Question

In series LR circuit ${X_L}$ = R and power factor of the circuit is ${P_1}$ when capacitor with capacitance C such that ${X_L} = {X_C}$ is put in series, the power factor becomes ${P_2}$ calculate $\dfrac{{{P_1}}}{{{P_2}}}$

Answer 1

Hint: This is the content of Before finding the ratio of power factor in RL circuit to that of RLC circuit firstly we will define the term power factor R,L,C are nothing but the passive elements present in electrical circuits and either dissipates or store the electrical energy .

Complete step-by-step answer:
Impedance- impedance is the measure of the opposition presented by a circuit to a current when applying a voltage. Impedance extends the resistance concept to circuits with alternating current (AC). Impedance has both magnitude and phase, unlike resistance which has magnitude only.
It is denoted by Z.
RL circuit- It is a first-order circuit, composed of one resistor and an inductor.

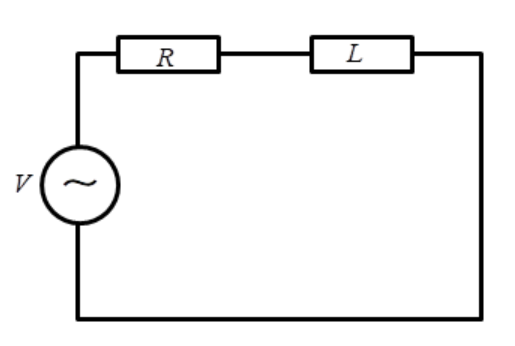
The impedance for RL circuit is given by
$Z = \sqrt {{R^2} + {{\left( {\omega L} \right)}^2}} $
Whereas, RLC circuit- it is the network of electrical elements in which resistor, inductor and capacitor are present and it is of 2nd order.

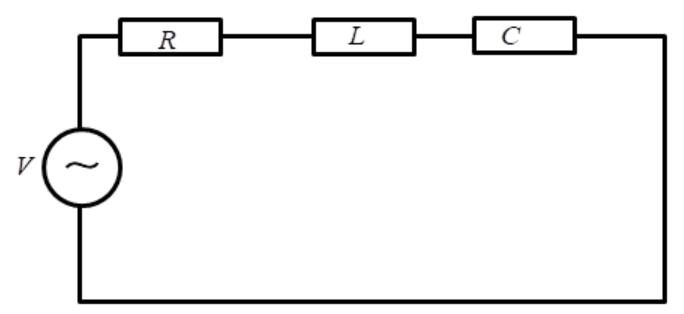
The impedance of RLC circuit is given by
$Z = \sqrt {{R^2} + {{\left( {\omega L} \right)}^2} + \dfrac{1}{{{{\left( {\omega C} \right)}^2}}}} $
Power Factor- It is defined as the ratio of the real power upon apparent power. The power closer to unity means more useful power and apart from unity means less useful power.
Given
${P_1}$ When $\left( {{X_L} = R} \right)$
Therefore, the power factor of the circuit is given by
${P_1} = \dfrac{R}{Z}$
Where
 ${P_1}$ is the power factor
Z is the impedance
$ \Rightarrow {P_1} = \dfrac{R}{{\sqrt {{R^2} + {X^2}} }} = \dfrac{R}{{\sqrt {2{R^2}} }} = \dfrac{1}{{\sqrt 2 }}$
New power factor ${P_2}$ when ${X_L} = {X_c}$
\[ {P_2} = \dfrac{R}{Z} \\
   \Rightarrow {P_2} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{X_L} - {X_c}} \right)}^2}} }} = \dfrac{R}{R} = 1 \\ \]
Thus
$\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{1}{{\sqrt 2 }}$
Hence, the ration of the power factor is $\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{1}{{\sqrt 2 }}$.

Note: Resonance condition for a series RLC circuit is achieved when the magnitude of capacitive reactance and inductive reactance are equal in magnitude but they are 180 degree apart in phase. In tuning applications, the sharp minimum impedance is useful. Power factor (PF) is the ratio of working power to the apparent power. Apparent power, also known as demand, is the measure of the amount of power used to run machinery and equipment during a certain period. It is found by multiplying. The result is expressed as kVA units.