Question

In a double slit experiment, when a thin film of thickness t having refractive index $\mu $ is introduced in front of one of the slits, the maximum at the centre of the fringe pattern shifts by one fringe width. The value of t is ($\lambda $ is the wavelength of the light used):
A. $\dfrac{\lambda }{2\left( \mu -1 \right)}$
B. $\dfrac{\lambda }{\left( 2\mu -1 \right)}$
C. $\dfrac{2\lambda }{\left( \mu -1 \right)}$
D. $\dfrac{\lambda }{\left( \mu -1 \right)}$

Answer 1

Hint: You could first correctly grasp the given information in the question and thus find a condition that would direct us to the required expression. You could also draw a neat diagram for YDSE as per the given condition for better clarity. Then you could do necessary rearrangements and substitutions to get the answer.

Complete step by step solution:
In the absence of any thin films Young’s double slit experiment would look something like this.

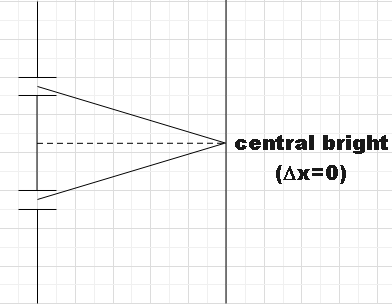
In the question, we are told that a thin film of thickness t is being introduced in front of one of the slits as a result of which the central bright is being shifted by one fringe width. So the YDSE would look something like this now.

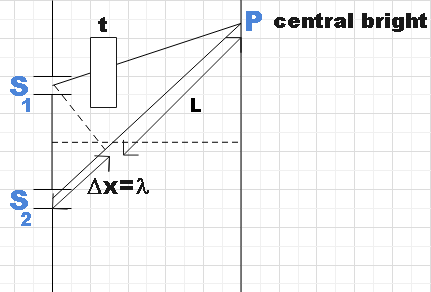
F or the central bright being shifted by one fringe width we could say that,
${{S}_{2}}P-{{S}_{1}}P=0$ …………………………….. (1)
From the figure,
${{S}_{2}}P=\lambda +L$
${{S}_{1}}P=L-t+\mu t$
Where, $\mu t$ is the extra path travelled by the light from slit ${{S}_{1}}$ due to the introduction of the thin film.
 Now (1) becomes,
$\left( \lambda +L \right)-\left( L-t+\mu t \right)=0$
$\Rightarrow \lambda +L-L+t-\mu t=0$
$\Rightarrow t\left( \mu -1 \right)=\lambda $
$\therefore t=\dfrac{\lambda }{\mu -1}$
Thus, we found the required expression to be,
$t=\dfrac{\lambda }{\mu -1}$
Hence, option D is the correct answer.

Note: You could simply make use of the diagram to find the optical path difference and then you should apply some conditions as per requirement. One significant point is to include the extra path covered by light from the slit 1 due to the thin film. Central fringe is defined as the bright fringe at n=0 with other fringes situated symmetrically about it.