Question

If Vector \[\overrightarrow {AB} = 2\hat i - \hat j + \hat k\] & \[\overrightarrow {OB} = 3\hat i - 4\hat j + 4\hat k\], finds the position vector \[\overrightarrow {OA} \].

Answer 1

Hint: A quantity having magnitude as well as direction is known as vector, necessary for finding the position of one point in space with respect to others. Vectors are represented by a line symbol \[ \to \]on the top of the variable that determines the magnitude and direction of the quantity.
Position vector is used to describe the position of a point relative to a point and as the point moves the position vector will change its direction or the length or the both. Position vector is described for a straight line whose one end is fixed to a body and the other end is a moving point. A position vector is also known as the location vector or the radius vector.
In this question we have to find the position vector of \[\overrightarrow {OA} \] by using the triangle law of addition of the vector.

Complete step by step solution: Given the vectors
\[\overrightarrow {AB} = 2\hat i - \hat j + \hat k\]
\[\overrightarrow {OB} = 3\hat i - 4\hat j + 4\hat k\]

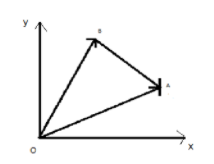
The position vector of \[\overrightarrow {OA} \]the straight line point where \[O\]is a fixed point and \[A\]is the moving point, here the vectors make a triangle hence we will use triangle law of vector addition which states when the two sides of triangle represent magnitude and direction then its third side will represent the magnitude and direction of their sum hence we can write \[\overrightarrow {OA} = \overrightarrow {AB} + \overrightarrow {OB} \], so the position vector of \[\overrightarrow {OA} \] is equal to
\[
  \overrightarrow {OA} = \overrightarrow {AB} + \overrightarrow {OB} \\
   = 2\hat i - \hat j + \hat k + 3\hat i - 4\hat j + 4\hat k \\
   = \left( {2 + 3} \right)\hat i + \left( { - 1 - 4} \right)\hat j + \left( {1 + 4} \right)\hat k \\
   = 5\hat i - 5\hat j + 5\hat k \\
 \]
Hence the position vector of \[\overrightarrow {OA} \] \[ = 5\hat i - 5\hat j + 5\hat k\]

Note: Resultant of a vector is the sum of two or more vectors it is the result of adding two or more vectors where if displacement vectors are added then the result is the resultant vector.