
If the area bounded by the x-axis, curve y = f (x) and the lines x = 1, x = b is equal to $ \sqrt{{{b}^{2}}+1}-\sqrt{2} $ for all b > 1, then f (x) is
a. $ \sqrt{x-1} $
b. $ \sqrt{x+1} $
c. $ \sqrt{{{x}^{2}}+1} $
d. $ \dfrac{x}{\sqrt{1+{{x}^{2}}}} $
Answer
580.2k+ views
Hint: We will first find the value of f (x) by generalizing the given relation, $ \int\limits_{1}^{b}{f\left( x \right)dx}=\sqrt{{{b}^{2}}+1}-\sqrt{2} $ and then we will differentiate the obtained general term to get the value of f (x).
Complete step-by-step answer:
It is given in the question that the area bounded by the x-axis, curve y = f (x) and the lines x = 1, x = b is equal to $ \sqrt{{{b}^{2}}+1}-\sqrt{2} $ for all b > 1 and we have been asked to find the value of f (x).
We can represent the given data as follows.
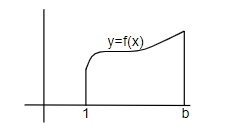
We know that the area under the curve y = (x) and x-axis is given by the integration of y = f (x) from 1 to b, as we have the lines x = 1 and x = b. So, we get,
Area = $ \int\limits_{1}^{b}{f\left( x \right)} $
Now, we have been given that $ \int\limits_{1}^{b}{f\left( x \right)dx} $ is equal to $ \sqrt{{{b}^{2}}+1}-\sqrt{2} $ , so we can write,
$ \int\limits_{1}^{b}{f\left( x \right)dx}=\sqrt{{{b}^{2}}+1}-\sqrt{2} $
We can also write $ \sqrt{2} $ as $ \sqrt{1+1} $ . So, we get,
$ \int\limits_{1}^{b}{f\left( x \right)dx}=\sqrt{{{b}^{2}}+1}-\sqrt{1+1} $
Now, if we observe $ \sqrt{{{b}^{2}}+1}-\sqrt{1+1} $ , we get to know that we can generalize it using the general function $ \left[ \sqrt{{{x}^{2}}+1} \right]_{1}^{b} $ , so we get,
$ \int\limits_{1}^{b}{f\left( x \right)dx}=\left[ \sqrt{{{x}^{2}}+1} \right]_{1}^{b} $
We know that integration is the reverse of differentiation, so we can write it as,
$ f\left( x \right)=\dfrac{d\left( \sqrt{{{x}^{2}}+1} \right)}{dx} $
Now, we will differentiate $ \left( \sqrt{{{x}^{2}}+1} \right) $ with respect to x. We know that the derivative of $ \sqrt{x} $ is $ \dfrac{1}{2\sqrt{x}} $ . So, we can write the derivative of $ \left( \sqrt{{{x}^{2}}+1} \right) $ as,
$ \begin{align}
& f\left( x \right)=\dfrac{1}{2\sqrt{{{x}^{2}}+1}}\times 2x \\
& f\left( x \right)=\dfrac{x}{\sqrt{{{x}^{2}}+1}} \\
\end{align} $
So, the correct answer is “Option D”.
Note: Many time, the students take the opposite limit after generalizing the function, f (x), they may take the function, $ \int{f\left( x \right)dx}=\left[ \sqrt{{{x}^{2}}+1} \right]_{b}^{1} $ which gives the opposite result. They might get a negative sign in the area of the region found out, but it is also correct as we will neglect the negative sign because the area cannot be negative.
Complete step-by-step answer:
It is given in the question that the area bounded by the x-axis, curve y = f (x) and the lines x = 1, x = b is equal to $ \sqrt{{{b}^{2}}+1}-\sqrt{2} $ for all b > 1 and we have been asked to find the value of f (x).
We can represent the given data as follows.
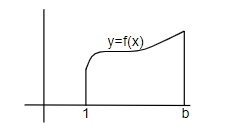
We know that the area under the curve y = (x) and x-axis is given by the integration of y = f (x) from 1 to b, as we have the lines x = 1 and x = b. So, we get,
Area = $ \int\limits_{1}^{b}{f\left( x \right)} $
Now, we have been given that $ \int\limits_{1}^{b}{f\left( x \right)dx} $ is equal to $ \sqrt{{{b}^{2}}+1}-\sqrt{2} $ , so we can write,
$ \int\limits_{1}^{b}{f\left( x \right)dx}=\sqrt{{{b}^{2}}+1}-\sqrt{2} $
We can also write $ \sqrt{2} $ as $ \sqrt{1+1} $ . So, we get,
$ \int\limits_{1}^{b}{f\left( x \right)dx}=\sqrt{{{b}^{2}}+1}-\sqrt{1+1} $
Now, if we observe $ \sqrt{{{b}^{2}}+1}-\sqrt{1+1} $ , we get to know that we can generalize it using the general function $ \left[ \sqrt{{{x}^{2}}+1} \right]_{1}^{b} $ , so we get,
$ \int\limits_{1}^{b}{f\left( x \right)dx}=\left[ \sqrt{{{x}^{2}}+1} \right]_{1}^{b} $
We know that integration is the reverse of differentiation, so we can write it as,
$ f\left( x \right)=\dfrac{d\left( \sqrt{{{x}^{2}}+1} \right)}{dx} $
Now, we will differentiate $ \left( \sqrt{{{x}^{2}}+1} \right) $ with respect to x. We know that the derivative of $ \sqrt{x} $ is $ \dfrac{1}{2\sqrt{x}} $ . So, we can write the derivative of $ \left( \sqrt{{{x}^{2}}+1} \right) $ as,
$ \begin{align}
& f\left( x \right)=\dfrac{1}{2\sqrt{{{x}^{2}}+1}}\times 2x \\
& f\left( x \right)=\dfrac{x}{\sqrt{{{x}^{2}}+1}} \\
\end{align} $
So, the correct answer is “Option D”.
Note: Many time, the students take the opposite limit after generalizing the function, f (x), they may take the function, $ \int{f\left( x \right)dx}=\left[ \sqrt{{{x}^{2}}+1} \right]_{b}^{1} $ which gives the opposite result. They might get a negative sign in the area of the region found out, but it is also correct as we will neglect the negative sign because the area cannot be negative.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




