
If $A$ and \[B\] are two events, then \[P(A\cup B)=\]
A. \[P(A)+P(B)\]
B. \[P(A)+P(B)+P(A\cap B)\]
C. \[P(A)+P(B)-P(A\cap B)\]
D. \[P(A)\cdot P(B)\]
Answer
233.1k+ views
Hint: In this question, we are to find the probability of the union of two events. This is nothing but proof of the addition theorem on probability. By using set theory, the required probability is calculated.
Formula Used:The probability is calculated by,
\[P(E)=\dfrac{n(E)}{n(S)}\]
\[n(E)\] - favourable outcomes and \[n(S)\] - sample.
According to set theory,
the Union of sets is described as
\[A\cup B=\{x/x\in A\text{ or }x\in B\}\]
Intersection of sets is described as
\[A\cap B=\{x/x\in A\text{ and }x\in B\}\]
Symmetric difference is described as
\[\begin{align}
& A-B=\{x/x\in A\text{ and }x\notin B\} \\
& B-A=\{x/x\in B\text{ and }x\notin A\} \\
\end{align}\]
If there are two events in a sample space, then the addition theorem on probability is given by
\[P(A\cup B)=P(A)+P(B)-P(A\cap B)\]
Complete step by step solution:Consider two events $A$ and \[B\].
These events are shown by the Venn diagram as below:
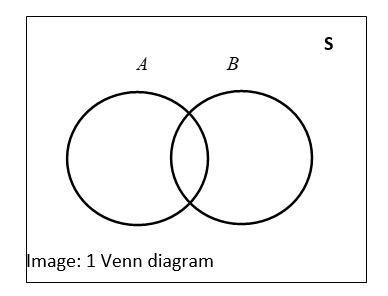
From the diagram, we have
\[\begin{align}
& A\cup B=S \\
& (B-A)\cup (A\cap B)=B \\
& (B-A)A\cap (B-A)=\Phi \\
& A\cup (B-A)=A\cup B \\
& A\cap (A\cap B)=\Phi \\
\end{align}\]
Then, from these we can apply probability on \[(B-A)\cup (A\cap B)=B\] and \[A\cup (B-A)=A\cup B\].
Applying probability to \[(B-A)\cup (A\cap B)=B\]:
\[\begin{align}
& (B-A)\cup (A\cap B)=B \\
& P(B)=P\left[ (B-A)\cup (A\cap B) \right] \\
& \text{ }=P(B-A)+P(A\cap B) \\
& \Rightarrow P(B-A)=P(B)-P(A\cap B)\text{ }...(1) \\
\end{align}\]
Applying probability to \[A\cup (B-A)=A\cup B\]:
\[\begin{align}
& A\cup (B-A)=A\cup B \\
& P(A\cup B)=P\left[ A\cup (B-A) \right] \\
& \text{ }=P(A)+P(B-A) \\
\end{align}\]
On substituting (1), we get
\[P(A\cup B)==P(A)+P(B)-P(A\cap B)\]
Thus, the addition theorem on probability is proved.
Option ‘C’ is correct
Note: Here we may go wrong with the set theory formula. If the Venn diagram is used, then the formulae will be established easily. Then, by applying the probability to the sets, the required addition theorem on probability is obtained.
Formula Used:The probability is calculated by,
\[P(E)=\dfrac{n(E)}{n(S)}\]
\[n(E)\] - favourable outcomes and \[n(S)\] - sample.
According to set theory,
the Union of sets is described as
\[A\cup B=\{x/x\in A\text{ or }x\in B\}\]
Intersection of sets is described as
\[A\cap B=\{x/x\in A\text{ and }x\in B\}\]
Symmetric difference is described as
\[\begin{align}
& A-B=\{x/x\in A\text{ and }x\notin B\} \\
& B-A=\{x/x\in B\text{ and }x\notin A\} \\
\end{align}\]
If there are two events in a sample space, then the addition theorem on probability is given by
\[P(A\cup B)=P(A)+P(B)-P(A\cap B)\]
Complete step by step solution:Consider two events $A$ and \[B\].
These events are shown by the Venn diagram as below:

From the diagram, we have
\[\begin{align}
& A\cup B=S \\
& (B-A)\cup (A\cap B)=B \\
& (B-A)A\cap (B-A)=\Phi \\
& A\cup (B-A)=A\cup B \\
& A\cap (A\cap B)=\Phi \\
\end{align}\]
Then, from these we can apply probability on \[(B-A)\cup (A\cap B)=B\] and \[A\cup (B-A)=A\cup B\].
Applying probability to \[(B-A)\cup (A\cap B)=B\]:
\[\begin{align}
& (B-A)\cup (A\cap B)=B \\
& P(B)=P\left[ (B-A)\cup (A\cap B) \right] \\
& \text{ }=P(B-A)+P(A\cap B) \\
& \Rightarrow P(B-A)=P(B)-P(A\cap B)\text{ }...(1) \\
\end{align}\]
Applying probability to \[A\cup (B-A)=A\cup B\]:
\[\begin{align}
& A\cup (B-A)=A\cup B \\
& P(A\cup B)=P\left[ A\cup (B-A) \right] \\
& \text{ }=P(A)+P(B-A) \\
\end{align}\]
On substituting (1), we get
\[P(A\cup B)==P(A)+P(B)-P(A\cap B)\]
Thus, the addition theorem on probability is proved.
Option ‘C’ is correct
Note: Here we may go wrong with the set theory formula. If the Venn diagram is used, then the formulae will be established easily. Then, by applying the probability to the sets, the required addition theorem on probability is obtained.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding the Electric Field of a Uniformly Charged Ring

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Derivation of Equation of Trajectory Explained for Students

Understanding Electromagnetic Waves and Their Importance

Understanding How a Current Loop Acts as a Magnetic Dipole

Understanding Average and RMS Value in Electrical Circuits




