Question

Find the total resistance across AB. Given R=$160\sqrt 3 \Omega $.

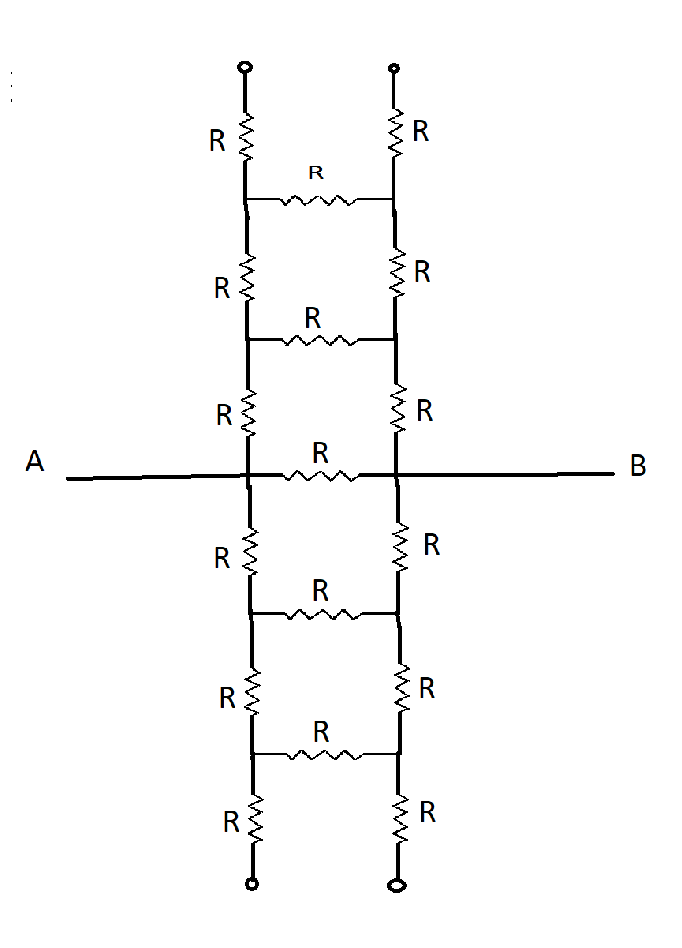
Answer 1

Hint: 1. This is the recurring circuit where resistance keeps on increasing from the two ends.
2. In series connection the current flows through one resistance then through other resistance hence the total resistance is the sum of both.
3. In a parallel connection, an equivalent Connection is given by \[\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_{}}}} + \dfrac{1}{{{R_2}}}\].

Complete step by step solution:
Here we need to find the equivalent resistance across A and B
Here we can see that the resistance circuit is symmetrical to AB


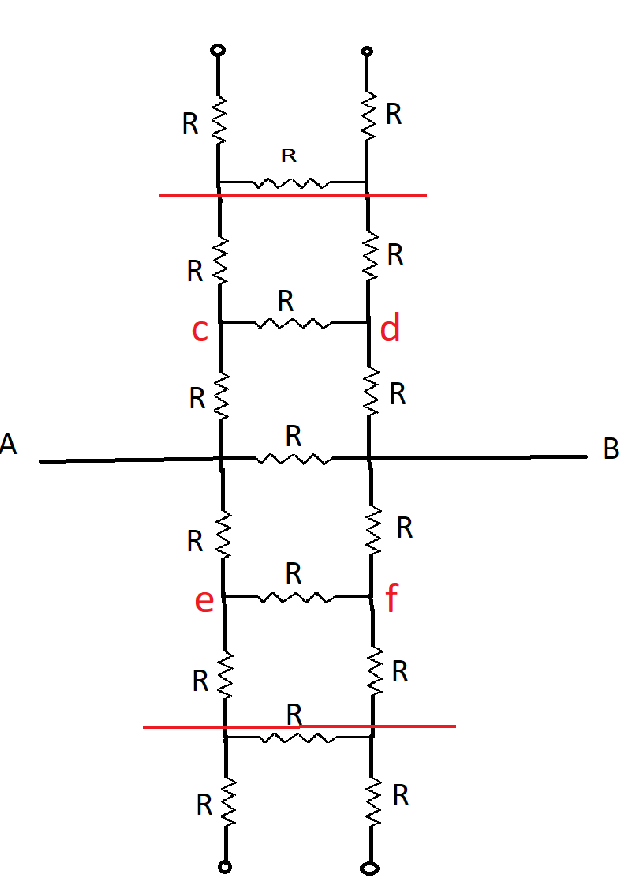
Here we can see that the circuit is infinite and repeats itself above (cd)and below (ef)
The top three resistance marked above the red line are taken as ${R_{eq}}$ the same case is at the bottom also and their values will also be the same, so we substitute ${R_{eq}}$in place of them. So now our image looks like


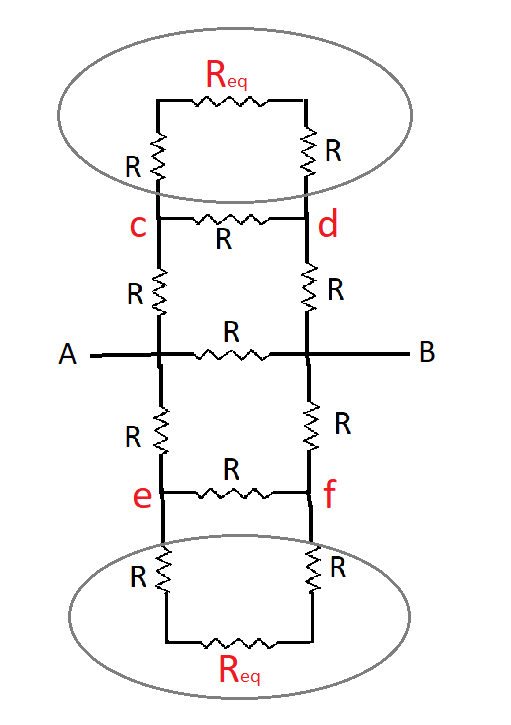
The resistance in top and bottom circles shows series connections so their equivalent resistance is given by
$
  {R_{eq`}} = {R_{eq}} + R + R \\
  \therefore {R_{eq`}} = {R_{eq}} + 2R \\
 $
Now our equivalent diagram looks like


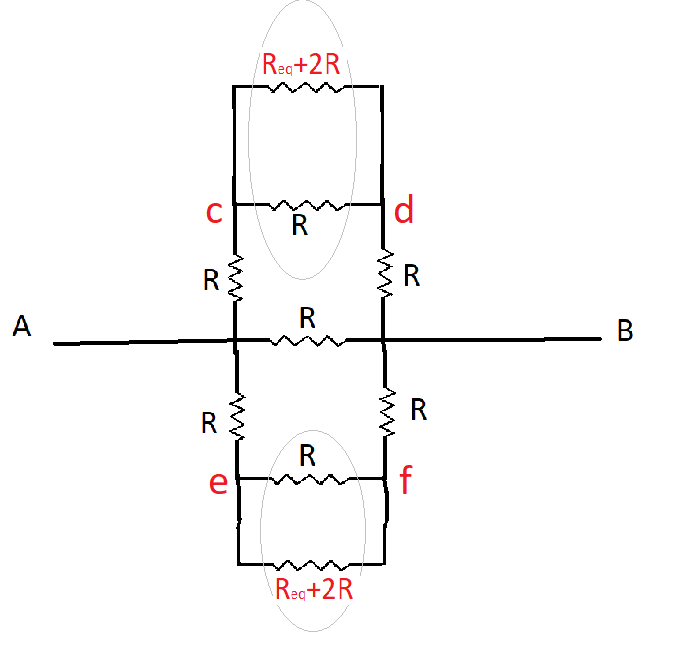
The resistance inside the circle are in parallel so there equivalent will be
\[
  {R_{eq}} = \dfrac{{\left( {{\operatorname{R} _{eq}} + 2R} \right)R}}{{{\operatorname{R} _{eq}} + 2R + R}} \\
   \Rightarrow {R_{eq}} = \dfrac{{\left( {R \times {\operatorname{R} _{eq}} + 2{R^2}} \right)}}{{{\operatorname{R} _{eq}} + 3R}} \\
   \Rightarrow {R_{eq}}^2 + 3R\left( {{R_{eq}}} \right) = {R_{eq}} \times R + 2{R^2} \\
   \Rightarrow {R_{eq}}^2 + 2R{R_{eq}} - 2{R^2} = 0 \\
   \Rightarrow {R_{eq}}^2 - 2{R^2} + 2R{R_{eq}} = 0 \\
 \]
Solving the above quadratic equation we get
\[
  {R_{eq}} = \dfrac{{ - 2R \pm \sqrt {4{R^2} - 8{R^2}} }}{2} \\
   \Rightarrow {R_{eq}} = - R + \sqrt 3 R \\
   \Rightarrow {R_{eq}} = \left( {\sqrt 3 - 1} \right)R \\
 \]
Now our equivalent circuit looks like


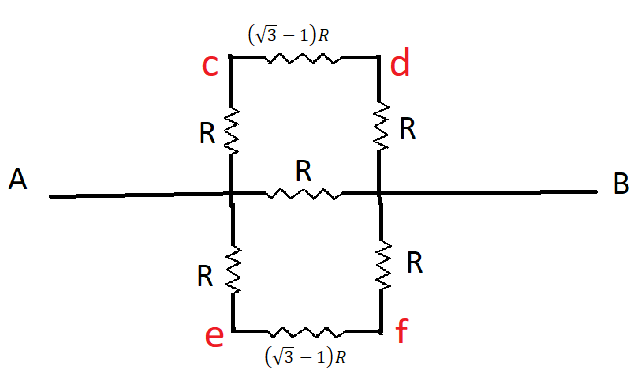
Now we see all the resistance above AB are in series so
The total resistance on each side will be
\[
  {R_{eq}} = \left( {\sqrt 3 - 1} \right)R + 2R \\
  \therefore {R_{eq}} = \left( {\sqrt 3 + 1} \right)R \\
 \]
Now finally our circuit diagram looks like


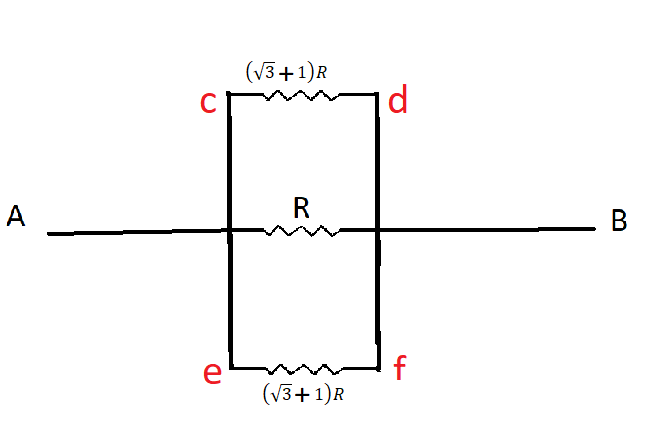
Here we can see that resistance on either side of AB are equal and parallel
AS we know two equivalent resistance of two equal resistance in parallel is half of the resistance of any one side so
${R_{eq}} = \dfrac{{\left( {\sqrt 3 + 1} \right)R}}{2}$
So final resistance will be
\[
  {R_{eq}} = \dfrac{{\left( {\sqrt 3 + 1} \right)\dfrac{R}{2} \times R}}{{\left( {\sqrt 3 + 1} \right)\dfrac{R}{2} + R}} \\
   \Rightarrow {R_{eq}} = \dfrac{{\left( {\sqrt 3 + 1} \right)\dfrac{R}{2}}}{{\left( {\sqrt 3 + 1} \right)\dfrac{1}{2} + 1}} \\
   \Rightarrow {R_{eq}} = \dfrac{{\left( {\sqrt 3 + 1} \right)R}}{{\left( {\sqrt 3 + 3} \right)}} \\
   \Rightarrow {R_{eq}} = \dfrac{{\left( {\sqrt 3 + 1} \right)R}}{{\sqrt 3 \left( {1 + \sqrt 3 } \right)}} \\
   \Rightarrow {R_{eq}} = \dfrac{R}{{\sqrt 3 }} \\
 \]
Here we are given that $R = 160\sqrt 3 \Omega $
Substituting this value we get
$
  {R_{eq}} = \dfrac{{160\sqrt 3 }}{{\sqrt 3 }} \\
  \therefore {R_{eq}} = 160\Omega \\
 $

Final answer is, The equivalent resistance of the above circuit will be $160\Omega$.

Note: In these questions the assumption for ${R_{eq}}$ the repeating resistance which was initially present at top and bottom is necessary.
In Series connection, the current is not divided but in parallel connection, it is divided
In a series connection, if one resistance fails then the circuit will be broken which is not in the case of parallel connection as the current will keep flowing from the other branch.