Question

Find the distance of the point \((2,\,3,\, - 5)\)from the plane\(x + 2y - 2z = 9.\)

a) 4
b) 3
c) 2
d) 1

Answer 1

Hint: The distance of a point from the plane represents the shortest distance or the perpendicular distance between the point and the plane.



Formula Used:


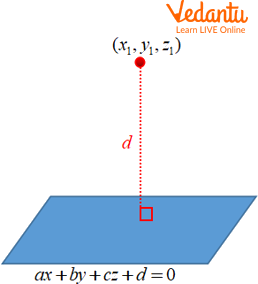
The perpendicular distance of the point \(({x_1},{y_1},{z_1})\)from the plane \(ax + by + cz + d = 0\)is \(d = \left| {\dfrac{{a{x_1} + b{y_1} + c{z_1} + d}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}} \right|\)







Complete step by step solution:Let us rewrite the given equation of the plane in general form.

\(x + 2y - 2z - 9 = 0\)

Here,\(({x_1},{y_1},{z_1}) = (2,\,3,\, - 5)\), \(a = 1,\,b = 2,\,c = - 2\,\,{\rm{and}}\,\,d = - 9.\)

Perpendicular distance of the point \((2,\,3,\, - 5)\)from the plane\(x + 2y - 2z - 9 = 0\)

\( = \left| {\dfrac{{(1)(2) + (2)(3) + ( - 2)( - 5) - 9}}{{\sqrt {{1^2} + {2^2} + {{( - 2)}^2}} }}} \right|\)

\( = \left| {\dfrac{{2 + 6 + 10 - 9}}{{\sqrt {1 + 4 + 4} }}} \right|\)

\( = \left| {\dfrac{9}{{\sqrt 9 }}} \right|\)

\( = \dfrac{9}{3}\)

= 3



Option ‘B’ is correct


Note: This problem can also be solved using the following method.

The direction ratio of the normal to the plane \(x + 2y - 2z - 9 = 0\) is (1, 2, -2).

Since the required line is perpendicular to the plane, then the direction ratio of the normal to the plane is same as the direction ratio of the line. (Sine the line is parallel to the normal.)

Equation of the straight line passing through the point \(({x_1},{y_1},{z_1})\) and having the direction ratios of parallel vector (a, b, c) is given by

\(\dfrac{{x - {x_1}}}{a} = \dfrac{{y - {y_1}}}{b} = \dfrac{{z - {z_1}}}{c}\)

The required line is passing through the point \((2,\,3,\, - 5)\) and having the direction ratio of parallel vector (1, 2, -2) is

\(\dfrac{{x - 2}}{1} = \dfrac{{y - 3}}{2} = \dfrac{{z + 5}}{{ - 2}}\) ----(1)

Any point on the line is of the form

\(\dfrac{{x - 2}}{1} = \dfrac{{y - 3}}{2} = \dfrac{{z + 5}}{{ - 2}} = k\)

\(\dfrac{{x - 2}}{1} = k\)

\(x = k + 2\)
\(\dfrac{{y - 3}}{2} = k\)

\(y = 2k + 3\)
\(\dfrac{{z + 5}}{{ - 2}} = k\)

\(z = - 2k - 5\)


So, any point on the line is\((k + 2,2k + 3, - 2k - 5)\).

The above point lies on the plane \(x + 2y - 2z - 9 = 0\) as equation (1) is perpendicular to the plane.

\( \Rightarrow k + 2 + 2\left( {2k + 3} \right) - 2\left( { - 2k - 5} \right) - 9 = 0\)

                \(k + 2 + 4k + 6 + 4k + 10 - 9 = 0\)

                                                \(9k + 9 = 0\)

                                                       \(k = 1\)

Therefore, the point on the plane\(x + 2y - 2z - 9 = 0\) is given by

\( \Rightarrow (1 + 2,2\left( 1 \right) + 3, - 2\left( 1 \right) - 5)\)

\( \Rightarrow (3,5, - 7)\)

Hence, the required distance be the distance between\((2,\,3,\, - 5)\)and\((3,5, - 7)\).

Required distance \[ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} \]


                              \[ = \sqrt {{{\left( {3 - 2} \right)}^2} + {{\left( {5 - 3} \right)}^2} + {{\left( { - 7 + 5} \right)}^2}} \]


                              \[ = \sqrt {{1^2} + {2^2} + {{\left( { - 2} \right)}^2}} \]

                              \[ = \sqrt 9 \]

                               = 3

So, the correct choice is b.