Question

Find the area of the ellipse \[25{x^2} + 4{y^2} = 100\].

Answer 1

Hint:In this question we have found the area of the ellipse. The equation of the ellipse is \[25{x^2} + 4{y^2} = 100\]. This is not in the standard form ellipse equation so we have to transform this equation to the form of ellipse equation. From that we have to find the coordinates of the ellipse.Let us consider, \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\], be the general form of an ellipse. So, the area of the ellipse is \[2\int\limits_{ - a}^a {b\sqrt {1 - \dfrac{{{x^2}}}{{{a^2}}}} } dx\].Simplifying we get area of ellipse.

Formula used:
Complete step-by-step answer:
It is given that; the equation of the ellipse is \[25{x^2} + 4{y^2} = 100\].
We have to find the area of the given ellipse.
It is not a general form of an ellipse equation. Hence we have transform the equation we get,
The equation of the ellipse can be written as, \[\dfrac{{25{x^2}}}{{100}} + \dfrac{{4{y^2}}}{{100}} = 1\].
On simplifying we get,
 \[\dfrac{{{x^2}}}{4} + \dfrac{{{y^2}}}{{25}} = 1\] … (1)

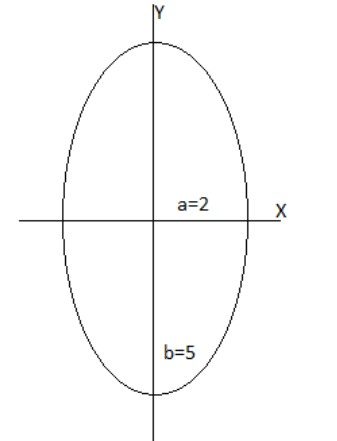
It means the ellipse cuts the X-axis and Y-axis at \[(2,0)\,\&\, (0,5)\] respectively.
To find the area of the ellipse, we have to take the limit from \[0\] to \[2\].
Let us solve equation (1) for y we get,
\[y = 5\sqrt {1 - \dfrac{{{x^2}}}{4}} \]
As in ellipse major and minor axis divides it into 4 parts
So, the area of the given ellipse becomes
\[A = \int\limits_0^2 {(4)5\sqrt {1 - \dfrac{{{x^2}}}{4}} } dx\]
Let us consider \[x = 2\sin t\]
Differentiate \[x\] with respect to \[t\], we can get, \[dx = 2\cos tdt\]
By substituting limit of \[x\] in \[x\] we get,
Limit from \[0\] to \[2\] changes from \[0\] to \[\dfrac{\pi }{2}\].
By substituting the above values we get,
\[A = \int\limits_0^{\dfrac{\pi }{2}} {(4)5\sqrt {1 - \dfrac{{4{{\sin }^2}t}}{4}} } 2\cos tdt\]
Let us now simplify the fractions in the above equation we get,
\[A = \int\limits_0^{\dfrac{\pi }{2}} {(2)(4)5\sqrt {1 - {{\sin }^2}t} } \cos tdt\]
We know that \[\cos t = \sqrt {1 - {{\sin }^2}t} \]
\[A = \int\limits_0^{\dfrac{\pi }{2}} {40\cos t\cos tdt} \]
Let us solve it further we get,
\[A = \int\limits_0^{\dfrac{\pi }{2}} {40{{\cos }^2}t} dt\]
We know that \[{\cos ^2}t = \dfrac{{1 + \cos 2t}}{2}\] substituting in the above equation, we get,
\[A = 40\int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{1 + \cos 2t}}{2}} dt\]
Simplifying we get,
\[A = 20\int\limits_0^{\dfrac{\pi }{2}} {(1 + \cos 2t)} dt\]
We know integration of $1$ is $t$ and $\cos 2t$ is ${\dfrac{\sin 2t}{2}}$
So,Integrating above equation we get,
\[A = 20{\left[ {t + {\dfrac{\sin 2t}{2}}} \right]^{\dfrac{\pi }{2}}}_0\]
Let substitute the limit we get,
\[A = 20[\dfrac{\pi }{2} + 0]\]
On simplifying we get,
\[A = 10\pi \]
Hence, the area of the given ellipse \[25{x^2} + 4{y^2} = 100\] is \[10\pi \].

Note:Students should remember integration,differentiation and trigonometric formulas for solving these types of questions.
The problem can be solved by another method.
Let us consider, \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\], be the general form of an ellipse. So, the area of the ellipse is \[4\int\limits_0^a {b\sqrt {1 - \dfrac{{{x^2}}}{{{a^2}}}} } dx = \pi ab\]
Here, \[a = 2,b = 5\]
Substitute the value in the above formula we get,
\[\pi \times 2 \times 5 = 10\pi \]
Hence, the area of the given ellipse \[25{x^2} + 4{y^2} = 100\] is \[10\pi \] sq.units.