Question

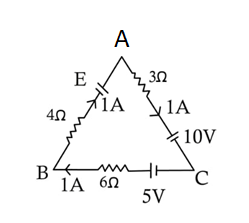
Find E for the given loop:

A) $-24 V$
B) $18V$
C) $4V$
D) $0V$

Answer 1

Hint: To solve this question, we need an equation which can relate the unknown and known voltages and the current and resistance, so that by solving it, we can obtain the unknown voltage E. The relationship between current, resistance and voltage is given by a law called Ohm’s law, which gives the mathematical expression:
$V = IR$
where V = voltage, I = current and R = resistance.

Complete step by step answer:
Consider the given loop ABC
For a continuous loop carrying current, Kirchoff’s voltage law is applicable.
The Kirchoff’s voltage law is based on the conservation of energy. As per the Kirchoff’s voltage law, the total electric energy of a mesh/loop should remain constant.
The Kirchoff’s voltage law states that –
The net voltage drop in the loop is equal to the net emf of the loop.
Here, voltage drop means the loss in electric voltage due to resistance. When current flows over a resistor, there is some voltage reduction, which is denoted as the voltage ‘dropped’ on the resistor.
The voltage drop on a resistor of resistance R when current I is flowing through is given by –
$V = IR$
The emf is the voltage provided by the cell or the battery in the circuit.
Before we apply Kirchoff's law to any loop, we have to consider the directions of the traverse and the current. If we go from A to C to B in the loop above, the voltage drop is taken positive if the current is in the same direction as that of the direction of traverse.
Also, during the traverse, the emf is considered positive if the jump is from negative terminal to positive terminal and vice-versa for negative.
In this loop, let us consider the direction of traverse as A – C – B.
Applying the Kirchoff’s law to the above loop ABC, we obtain –
$3 \times 1 + 6 \times 1 + 4 \times 1 = - 10 + 5 + E$
$ \Rightarrow 13 = - 5 + E$
$\therefore E = 13 + 5 = 18V$
Hence, the value of E is $18 V$.

Hence, the correct option is Option B.

Note: The Kirchoff’s voltage law is the second law of Kirchoff’s laws. The first law is called Kirchoff’s current law which states that currents can be added algebraically, across a node. This first law is based on the principle of conservation of charge.