Question

An electric dipole, consisting of two opposite charges of magnitude \[2\times {{10}^{-6}}~C\] each separated by a distance 3 cm is placed in an electric field of magnitude \[2\times {{10}^{5}}~N{{C}^{-1}}\] along the direction making ${{90}^{o}}$ with the field. Torque acting on the dipole is:
$\begin{align}
& \text{A}\text{. }12\times {{10}^{-1}} \\
& \text{B}\text{. }12\times {{10}^{-2}} \\
& \text{C}\text{.}12\times {{10}^{-3}} \\
& \text{D}\text{. }12\times {{10}^{-4}} \\
\end{align}$

Answer 1

Hint: Electric dipole has equal charges, but of opposite sign, at both the ends separated by some distance. The force due to the electric field experienced by both the charges will be same in magnitude, but the direction will be opposite. As we know, an equal and opposite couple of forces generate torque and hence, the dipole will experience some torque acting on it while placed in an external electric field. We will calculate the value of this torque by calculating the magnitude of force generated by the electric field and using the relation between the force, torque and the distance of separation.

Formula used:
Force applied by an electric field \[\overrightarrow{E}\] on a charge $q$: $\overrightarrow{F}=q\overrightarrow{E}$
Torque on a dipole of charges $q$ and $-q$ separated by a distance $d$ in an electric field \[\overrightarrow{E}\]: $\tau =qEd$.

Complete step by step answer:
An electric dipole is a combination of two equal and opposite charges separated by a finite distance. Direction of dipole is from negative charge to positive charge.
We have an electric dipole, consisting of two opposite charges of magnitude \[2\times {{10}^{-6}}~C\] each separated by a distance 3 cm,
Let, $q$ and $-q$ be the charges and $d$ be the distance between them.
So, $q=2\times {{10}^{-6}}~C$
And, $d=3\text{ }cm$
We will convert the distance in SI unit, i.e. meter
$d=3\text{ }cm=3\times {{10}^{-2}}m$
Now, the dipole is placed in an electric field magnitude \[2\times {{10}^{5}}~N{{C}^{-1}}\]along the direction making ${{90}^{o}}$ with the field.
$E=2\times {{10}^{5}}~N{{C}^{-1}}$
Force applied by an electric field \[\overrightarrow{E}\] on a charge $q$ is:
$\overrightarrow{F}=q\overrightarrow{E}$
For a positive charge, direction of force will be the same as for an electric field, but for a negative charge, direction of force will be opposite as for an electric field.
Magnitude of this force will be:
$F=qE$
Where,
$E$ is the magnitude of an electric field.

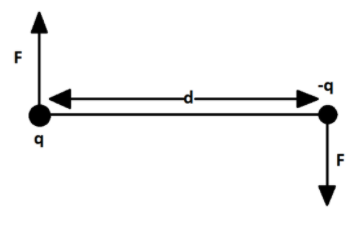
As we can see the magnitude of both the charges is the same, so magnitude of the force applied on the two charges will be the same, but the direction of forces will be opposite as one charge is positive and other is negative.
So, the two forces on dipole will cancel out each other, but we know that,
Equal and opposite forces separated by a finite distance applied on a body provide torque to the body.
Now, magnitude of torque applied by two equal and opposite forces of magnitude $F$ separated by a distance $d$ is:
$\tau =Fd$
Substituting $F=qE$ ,
We have:
$\tau =qEd$
Now, putting values
$q=2\times {{10}^{-6}}~C$
$d=3\times {{10}^{-2}}m$
$E=2\times {{10}^{5}}~N{{C}^{-1}}$
We get,
$\begin{align}
& \tau =\left( 2\times {{10}^{-6}}~C \right)\times \left( 2\times {{10}^{5}}~N{{C}^{-1}} \right)\times \left( 3\times {{10}^{-2}}m \right) \\
& \tau =12\times {{10}^{-6+5-2}}Nm \\
& \tau =12\times {{10}^{-3}}Nm \\
\end{align}$
The torque applied on the dipole by electric field is $12\times {{10}^{-3}}Nm$

So, the correct answer is “Option C”.

Note:
Students should note that the torque is generated only when the two forces acting on a body are equal in magnitude but opposite in the direction. Also, these forces must be separated by some distance. For a dipole, both the conditions are satisfied as the two charges are equal in magnitude, opposite in sign, and separated by some distance.