
A wire has linear resistance $\rho$(in Ohm/m). Find the resistance r between points A and B if the side of the larger square is ‘d’.
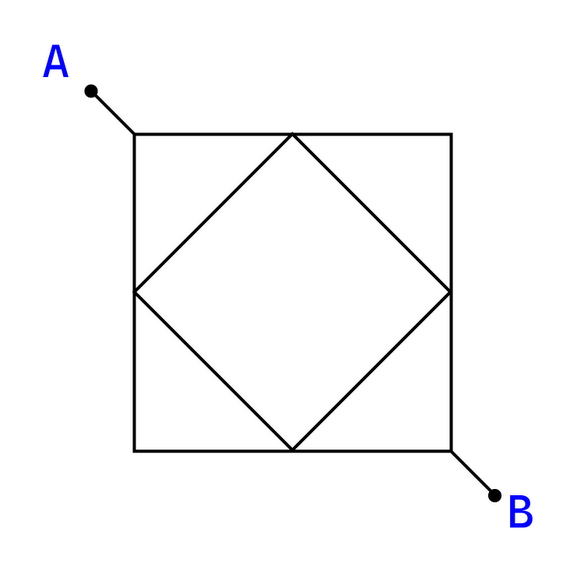
A) $\dfrac{\rho d}{\sqrt2}$
B) $\sqrt2\rho d$
C) $2rd$
D) None of these
Answer
232.8k+ views
Hint:The problem is from the electricity part of physics. We can apply the concept of parallel combination and series combination of resistance here. Use the equation for effective resistance in parallel and series combinations.
Formula Used:
Equivalent resistance for a series resistance circuit:
${R_E} = {R_1} + {R_2} + {R_3}$
Equivalent resistance for a parallel resistance circuit:
$\dfrac{1}{{{R_E}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}$
Where ${R_E}$= equivalent resistance and ${R_1},{R_2},{R_3}$ = component resistance.
Complete answer:
The equivalent resistance is a single resistance which can replace all the component resistances in a circuit in such a manner that the current in the circuit remains unchanged.
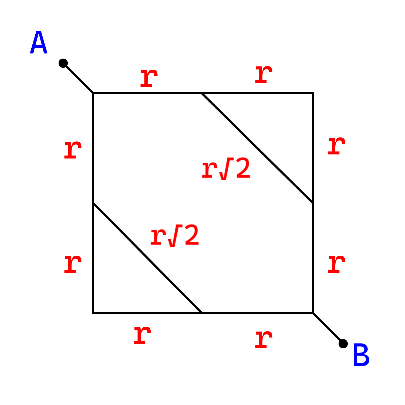
Figure 1
Let’s half side of the resistor is r. Where $r = \dfrac{{\rho d}}{2}$
We can redraw the circuit diagram and it will be.
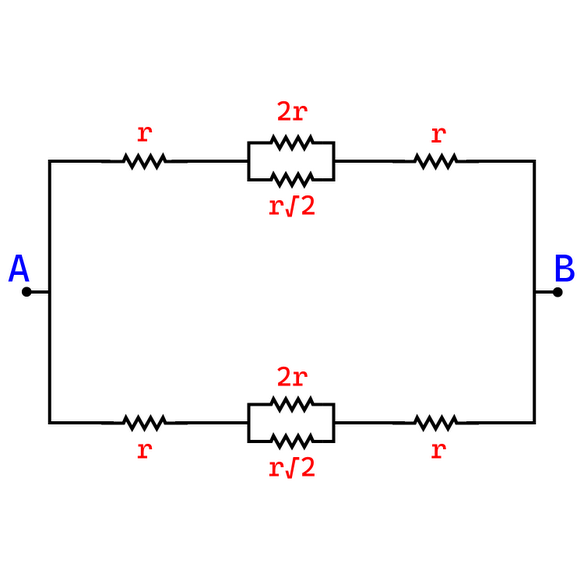
Figure 2
Apply the equations for parallel and series combinations and the equivalence resistance is calculated as,
${R_E} = \dfrac{1}{2}\left[ {2r + \dfrac{{2r \times r\sqrt 2 }}{{2r + r\sqrt 2 }}} \right] = \dfrac{1}{2}\left[ {2r + \dfrac{{2r \times r\sqrt 2 }}{{(2 + \sqrt 2 )r}}} \right]$
${R_E} = \dfrac{1}{2}\left[ {\dfrac{{2r \times (2 + \sqrt 2 )r + 2{r^2}\sqrt 2 }}{{(2 + \sqrt 2 )r}}} \right]$
${R_E} = \dfrac{1}{2}\left[ {\dfrac{{4r + 2r\sqrt 2 + 2r\sqrt 2 }}{{2 + \sqrt 2 }}} \right]$
${R_E} = \dfrac{1}{2}\left[ {\dfrac{{4r\sqrt 2 + 4r}}{{2 + \sqrt 2 }}} \right]$
${R_E} = \dfrac{{4r}}{2}\dfrac{{\sqrt 2 + 1}}{{2 + \sqrt 2 }} \times \dfrac{{2 - \sqrt 2 }}{{2 - \sqrt 2 }}$
${R_E} = 2r\left( {\dfrac{{2\sqrt 2 - {{(\sqrt 2 )}^2} + 2 - \sqrt 2 }}{{{2^2} - {{(\sqrt 2 )}^2}}}} \right)$
${R_E} = 2r\dfrac{{\sqrt 2 }}{2} = r\sqrt 2 $
Substituting the value of r and the ${R_E}$will become,
\[{R_E} = \dfrac{{\rho d\sqrt 2 }}{2} = \dfrac{{\rho d}}{{\sqrt 2 }}\]
Hence, the correct option is Option (A).
Note: Resistance is a measure of the opposition to current flow in an electrical circuit. Resistance blocks the flow of current. The S.I unit of resistance is ohms. The current decreases as resistance increases. On the other hand, the current increases as the resistance decreases. While solving this one also has to pay close attention to the connection between resistances.
Formula Used:
Equivalent resistance for a series resistance circuit:
${R_E} = {R_1} + {R_2} + {R_3}$
Equivalent resistance for a parallel resistance circuit:
$\dfrac{1}{{{R_E}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}$
Where ${R_E}$= equivalent resistance and ${R_1},{R_2},{R_3}$ = component resistance.
Complete answer:
The equivalent resistance is a single resistance which can replace all the component resistances in a circuit in such a manner that the current in the circuit remains unchanged.

Figure 1
Let’s half side of the resistor is r. Where $r = \dfrac{{\rho d}}{2}$
We can redraw the circuit diagram and it will be.

Figure 2
Apply the equations for parallel and series combinations and the equivalence resistance is calculated as,
${R_E} = \dfrac{1}{2}\left[ {2r + \dfrac{{2r \times r\sqrt 2 }}{{2r + r\sqrt 2 }}} \right] = \dfrac{1}{2}\left[ {2r + \dfrac{{2r \times r\sqrt 2 }}{{(2 + \sqrt 2 )r}}} \right]$
${R_E} = \dfrac{1}{2}\left[ {\dfrac{{2r \times (2 + \sqrt 2 )r + 2{r^2}\sqrt 2 }}{{(2 + \sqrt 2 )r}}} \right]$
${R_E} = \dfrac{1}{2}\left[ {\dfrac{{4r + 2r\sqrt 2 + 2r\sqrt 2 }}{{2 + \sqrt 2 }}} \right]$
${R_E} = \dfrac{1}{2}\left[ {\dfrac{{4r\sqrt 2 + 4r}}{{2 + \sqrt 2 }}} \right]$
${R_E} = \dfrac{{4r}}{2}\dfrac{{\sqrt 2 + 1}}{{2 + \sqrt 2 }} \times \dfrac{{2 - \sqrt 2 }}{{2 - \sqrt 2 }}$
${R_E} = 2r\left( {\dfrac{{2\sqrt 2 - {{(\sqrt 2 )}^2} + 2 - \sqrt 2 }}{{{2^2} - {{(\sqrt 2 )}^2}}}} \right)$
${R_E} = 2r\dfrac{{\sqrt 2 }}{2} = r\sqrt 2 $
Substituting the value of r and the ${R_E}$will become,
\[{R_E} = \dfrac{{\rho d\sqrt 2 }}{2} = \dfrac{{\rho d}}{{\sqrt 2 }}\]
Hence, the correct option is Option (A).
Note: Resistance is a measure of the opposition to current flow in an electrical circuit. Resistance blocks the flow of current. The S.I unit of resistance is ohms. The current decreases as resistance increases. On the other hand, the current increases as the resistance decreases. While solving this one also has to pay close attention to the connection between resistances.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26

Understanding the Electric Field of a Uniformly Charged Ring

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Derivation of Equation of Trajectory Explained for Students

Understanding Electromagnetic Waves and Their Importance




