Question

A vertical pole $PO$ is standing at the centre $O$ of a square $ABCD$. If $AC$ subtends an $\angle {90^ \circ }$ at the top $P$of the pole, then the angle subtended by a side of the square at $P$ is
1. ${30^ \circ }$
2. ${45^ \circ }$
3. ${60^ \circ }$
4. None of these

Answer 1

Hint:

 Start the solution by making figure of the given condition. In this question we have to find $\angle APB$. Let $a$ be the sides of the square. Now calculate the diameter of the given square using Pythagoras theorem. Applying trigonometry ratios find the value of the sides of $\Delta APB$ and you will know the value of angle.

Formula used:
Pythagoras theorem –
${\left( {Hypotenuse} \right)^2} = {\left( {Perpendicular} \right)^2} + {\left( {Base} \right)^2}$
Trigonometric ratio –
$\tan \theta = \dfrac{{Perpendicular}}{{Base}}$, $\sin \theta = \dfrac{{Perpendicular}}{{Hypotenuse}}$

Complete step by step solution:
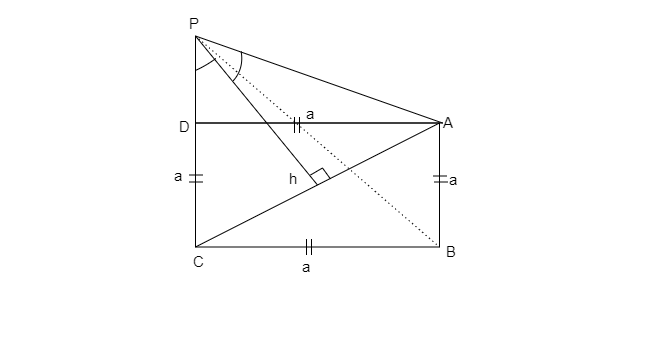
Let, the height of the pole $\left( {OP} \right)$ be $h$ and the sides of the square $ABCD$ be $a$
$ \Rightarrow AB = BC = CD = AD = a$
Also, draw a line joining the points $P$and $B$. Therefore $PB = PA$
Using Pythagoras theorem in $\Delta ABC$,
${\left( {AC} \right)^2} = {\left( {AB} \right)^2} + {\left( {BC} \right)^2}$
$ \Rightarrow AC = \sqrt 2 a$
OR $OA = OC = \dfrac{a}{{\sqrt 2 }}$
Given that,
$AC$ subtends an $\angle {90^ \circ }$ at the top $P$of the pole
$ \Rightarrow \angle OPA = \angle OPC = {45^ \circ }$
In $\Delta APO$,
$\tan {45^ \circ } = \dfrac{{OA}}{{OP}}$
$1 = \dfrac{{OA}}{{OP}}$
$OP = OA$
$h = \dfrac{a}{{\sqrt 2 }}$
And $\sin {45^ \circ } = \dfrac{{OA}}{{PA}}$
$\dfrac{1}{{\sqrt 2 }} = \dfrac{{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}}{{PA}}$
$PA = PB = a$
Here all the sides of $\Delta APB$ are equal.
$\Delta APB$ is an equilateral triangle
It implies that, $\angle APB = \angle PAB = \angle ABP = {60^ \circ }$
Hence, option (3) is the correct answer i.e., ${60^ \circ }$.

Note: The key concept involved in solving this problem is the good knowledge of applications of trigonometry. Students must know that trigonometry is one of the branches, which teaches us about the relationships between angles and sides of a triangle. To solve such questions, try to use $\sin \theta = \dfrac{{Perpendicular}}{{Hypotenuse}},\cos \theta = \dfrac{{Base}}{{Hypotenuse}},\tan \theta = \dfrac{{Perpendicular}}{{Base}}$ these formula in the required triangles or their reciprocals.