Question

A thin film of refractive index 1.5 and thickness \[4 \times {10^{ - 5}}cm\]illuminated by light normal to the surface. What wavelength within the visible spectrum will be intensified in the reflected beam?
A) 4800 \[\mathop A\limits^o \]
B) 5800 \[\mathop A\limits^o \]
C) 6000 \[\mathop A\limits^o \]
D) 6800 \[\mathop A\limits^o \]

Answer 1

Hint: When light falls on a thin film then it reflects back from two different surfaces. First, from the upper surface at the time of entering into the film some light reflects back. Then, at the other boundary where the light tries to exit from the film again it reflects back into the first medium. Now, this two reflected beams interfere due to the extra path length covered by the second reflected beam.




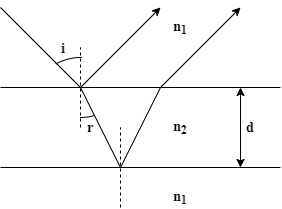
Formula Used: If a light ray reflects back while entering a denser medium from a rarer one its phase changes by an angle \[\pi \]. Hence, in case of thin film to have constructive interference required phase and path difference relation is given as:
$2d\dfrac{{{n_2}}}{{{n_1}}}\cos r = \left( {m - \dfrac{1}{2}} \right)\lambda $ (1)
Where,
d is the thickness of the film,
${n_2}$ is Refractive index(RI) of the film,
${n_1}$ is the refractive index of the rarer medium,
r is the angle of refraction,
m is order of interference,
$\lambda $ is the wavelength of interfering light

Complete step by step answer:
Given:
1. RI of the thin film is ${n_2} = 1.5$, where RI of air is ${n_1} = 1$.
2. Thickness of the thin film is \[d = 4 \times {10^{ - 5}}cm = 4 \times {10^{ - 7}}m\].
3. The light enters normally into the surface. Hence, \[i = r = {90^ \circ }\]. So, \[\cos r = \cos {90^ \circ } = 1\].

To find: The wavelength in the visible spectrum that will be intensified.

Step 1
First rewrite the eq.(1) to find an expression of $\lambda $:
$
  2d\dfrac{{{n_2}}}{{{n_1}}}\cos r = \left( {m - \dfrac{1}{2}} \right)\lambda \\
  \therefore \lambda = \dfrac{{2d{n_2}\cos r}}{{{n_1}\left( {m - \tfrac{1}{2}} \right)}} \\
 $ (2)

Step 2
Now, substitute the values of d, ${n_2}$and $\cos r$into eq.(2) to get the set of solutions for $\lambda $:
$\therefore \lambda = \dfrac{{2 \times 4 \times {{10}^{ - 7}} \times 1.5 \times 1}}{{1 \times \left( {m - \tfrac{1}{2}} \right)}}meter = \dfrac{{1.2 \times {{10}^{ - 6}}}}{{\left( {m - \tfrac{1}{2}} \right)}}meter = \dfrac{{12000}}{{\left( {m - \tfrac{1}{2}} \right)}}\mathop A\limits^o $
As the wavelength of visible light is within 3800\[\mathop A\limits^o \] to 7000\[\mathop A\limits^o \], so to get the wavelength within visible light range, the value of m must be 3. Then the intensified visible wavelength will be:
$\lambda = \dfrac{{12000}}{{\left( {3 - \tfrac{1}{2}} \right)}}\mathop A\limits^o = 12000 \times \dfrac{2}{5}\mathop A\limits^o = 4800\mathop A\limits^o $

Correct answer:
The wavelength within the visible spectrum that will be intensified in the reflected beam is (a) $4800\mathop A\limits^o $.


Note: While using the constructive interference condition a student might get confused noticing the fraction $\dfrac{1}{2}$ subtracted from m-th order. This phase subtraction is necessary to nullify an extra \[\pi \] phase difference that happens when light reflects back while travelling from rarer to denser medium.