Question

A point source of light is placed at a depth of $h$ below the surface of water of refractive index $\mu $. A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface. The minimum diameter of the disc is
A. $\dfrac{{2h}}{{{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}}$
B. $2h{({\mu ^2} - 1)^{\dfrac{1}{2}}}$
C. $\dfrac{h}{{2{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}}$
D. $h{({\mu ^2} - 1)^{\dfrac{1}{2}}}$

Answer 1

Hint: The light ray will refract back if the incidence angle becomes greater than the critical angle and hence we will use this concept to find the disc diameter. Use basic trigonometry to further solve the question.

Formula used:
${\theta _c} = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right) \\$

Complete Step-by-Step Explanation:


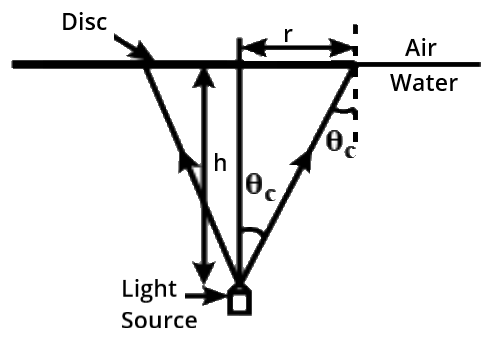
The above illustration depicts incidence from water at a critical angle ${\theta _c}$ limiting angle,
Consequently, the following formula provides the critical angle of a medium:
${\theta _c} = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right) \\$
 $\sin {\theta _c} = \dfrac{1}{\mu } \\$
So that, from the relation in the above equation, the equation can be written as:
$\tan {\theta _c} = \dfrac{1}{{{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}} \Rightarrow \dfrac{r}{h}$
Where, $r$be the radius of the disc,
Therefore, the diameter of the disc is:
$2r = 2h\,\tan {\theta _c} \\$
 $\Rightarrow d = \dfrac{{2h}}{{{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}} \\$
Thus, the correct option is: (A) $\dfrac{{2h}}{{{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}}$

Note: for such questions you should be clear with the concept of critical angle and basic laws of refraction. Remember when light goes from denser to rarer the snell’s law applied in opposite manner as compared to the one we study conventionally.