Question

A parabola is drawn to pass through \[A\] and \[B\], the ends of a diameter of a given circle of radius \[a\] and to have as directrix a tangent to a concentric circle of radius \[b\]; the axes being \[AB\] and a perpendicular diameter, prove that the locus of the focus of the parabola is \[\dfrac{{{x}^{2}}}{{{b}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}-{{a}^{2}}}=1\].

Answer 1

Hint: Any point on the parabola is equidistant from the focus and directrix.

Let the equation of the circle be \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}.....\left( i \right)\]
In the question, it is given that \[A\] and \[B\] are the ends of the diameter of the circle.

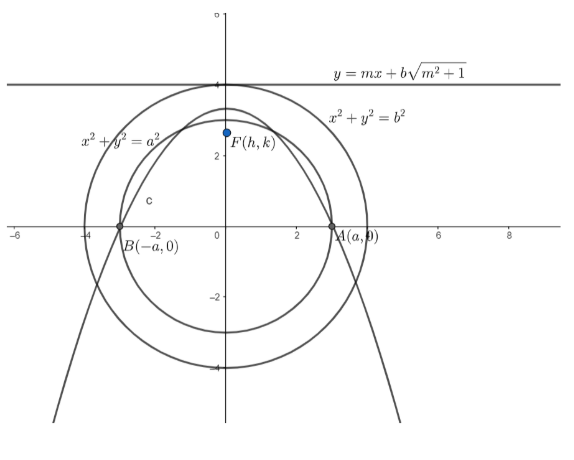
So, let \[A=\left( a,0 \right)\] and \[B=\left( -a,0 \right)\]
In the question, it is given that the radius of the concentric circle is \[b\].
So, let the equation of concentric circle be \[{{x}^{2}}+{{y}^{2}}={{b}^{2}}....\left( ii \right)\]
Now, the directrix of the parabola is tangent to the concentric circle.
First, we find the equation of tangent to the concentric circle.
We know, the equation of tangent to a circle \[{{x}^{2}}+{{y}^{2}}={{r}^{2}}\] in slope form is given as \[y=mx\pm r\sqrt{1+{{m}^{2}}}\].
So, equation of tangent to \[\left( ii \right)\]is
\[y=mx+b\sqrt{{{m}^{2}}+1}\]
Or \[mx-y+b\sqrt{{{m}^{2}}+1}=0....\left( iii \right)\]
Equation \[\left( iii \right)\] is also the directrix to the parabola.
Now, we want to find the locus of the focus of the parabola.
So, let the focus of the parabola be \[F\left( h,k \right)\].
Now, by the definition of a parabola, any point on the parabola is equidistant from the focus and the directrix.
Now, from the question, we know that the ends of diameter of \[\left( i \right)\]i.e. \[A\] and \[B\] lie on the parabola.
We know that the distance between two points \[({{x}_{1}},{{y}_{1}})\] and \[({{x}_{2}},{{y}_{2}})\] is given as \[d=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}\] and the distance of a point \[({{x}_{1}},{{y}_{1}})\] from the line \[lx+my+n=0\] is given
as \[d=\dfrac{l{{x}_{1}}+m{{y}_{1}}+n}{\sqrt{{{l}^{2}}+{{m}^{2}}}}\].
So, for \[A\left( a,0 \right)\], we have
\[\sqrt{{{\left( h-a \right)}^{2}}+{{k}^{2}}}=\dfrac{m\left( a \right)-1\left( 0 \right)+b\sqrt{{{m}^{2}}+1}}{\sqrt{{{m}^{2}}+1}}\]
\[\Rightarrow \sqrt{{{\left( h-a \right)}^{2}}+{{k}^{2}}}=\dfrac{am+b\sqrt{{{m}^{2}}+1}}{\sqrt{{{m}^{2}}+1}}....\left( iv \right)\]
For \[B\left( -a,0 \right)\], we have
\[\sqrt{{{\left( h+a \right)}^{2}}+{{k}^{2}}}=\dfrac{m\left( -a \right)-1\left( 0 \right)+b\sqrt{{{m}^{2}}+1}}{\sqrt{{{m}^{2}}+1}}\]
\[\Rightarrow \sqrt{{{\left( h+a \right)}^{2}}+{{k}^{2}}}=\dfrac{-am+b\sqrt{{{m}^{2}}+1}}{\sqrt{{{m}^{2}}+1}}....\left( v \right)\]
Adding \[\left( iv \right)\]and \[\left( v \right)\], we have
\[\sqrt{{{\left( h-a \right)}^{2}}+{{k}^{2}}}+\sqrt{{{\left( h+a \right)}^{2}}+{{k}^{2}}}=\dfrac{2b\sqrt{{{m}^{2}}+1}}{\sqrt{{{m}^{2}}+1}}\]
\[\Rightarrow \sqrt{{{\left( h-a \right)}^{2}}+{{k}^{2}}}+\sqrt{{{\left( h+a \right)}^{2}}+{{k}^{2}}}=2b\]
\[\sqrt{{{\left( h+a \right)}^{2}}+{{k}^{2}}}=2b-\sqrt{{{\left( h-a \right)}^{2}}+{{k}^{2}}}\]
Now, on squaring both sides we get,
\[{{h}^{2}}+2ah+{{a}^{2}}+{{k}^{2}}=4{{b}^{2}}+{{h}^{2}}-2ah+{{a}^{2}}+{{k}^{2}}-4b\sqrt{{{(h-a)}^{2}}+{{k}^{2}}}\]
\[\begin{align}
  & \Rightarrow 4{{b}^{2}}-4ah=4b\sqrt{{{(h-a)}^{2}}+{{k}^{2}}} \\
 & \Rightarrow {{b}^{2}}-ah=b\sqrt{{{(h-a)}^{2}}+{{k}^{2}}} \\
\end{align}\]
Now, let’s square both sides again to remove the square root sign. We get \[{{b}^{4}}+{{a}^{2}}{{h}^{2}}-2{{b}^{2}}ah={{b}^{2}}({{h}^{2}}-2ah+{{a}^{2}}+{{k}^{2}})\]
On dividing both sides with \[{{b}^{2}}\], we get
\[{{b}^{2}}+\dfrac{{{a}^{2}}{{h}^{2}}}{{{b}^{2}}}-2ah={{h}^{2}}-2ah+{{a}^{2}}+{{k}^{2}}\]
\[\Rightarrow {{b}^{2}}-{{a}^{2}}-{{k}^{2}}={{h}^{2}}-\dfrac{{{a}^{2}}{{h}^{2}}}{{{b}^{2}}}\]
\[\Rightarrow ({{b}^{2}}-{{a}^{2}})(1-\dfrac{{{k}^{2}}}{{{b}^{2}}-{{a}^{2}}})={{h}^{2}}(1-\dfrac{{{a}^{2}}}{{{b}^{2}}})\]
\[\Rightarrow ({{b}^{2}}-{{a}^{2}})(1-\dfrac{{{k}^{2}}}{{{b}^{2}}-{{a}^{2}}})={{h}^{2}}(\dfrac{{{b}^{2}}-{{a}^{2}}}{{{b}^{2}}})\]
\[\Rightarrow 1-\dfrac{{{k}^{2}}}{{{b}^{2}}-{{a}^{2}}}=\dfrac{{{h}^{2}}}{{{b}^{2}}}\]
\[\Rightarrow 1=\dfrac{{{h}^{2}}}{{{b}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}-{{a}^{2}}}\]
So, the locus of \[(h,k)\] is given by replacing \[(h,k)\]by \[(x,y)\]
So, the equation of the locus is given as \[\dfrac{{{x}^{2}}}{{{b}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}-{{a}^{2}}}=1\] \[\]\[\]

Note: The distance between two points \[({{x}_{1}},{{y}_{1}})\] and \[({{x}_{2}},{{y}_{2}})\] is given as \[d=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}\] and not \[d=\sqrt{{{({{x}_{1}}+{{x}_{2}})}^{2}}+{{({{y}_{1}}+{{y}_{2}})}^{2}}}\]. It is a very common mistake made by students.