Question

A man of height h walks in a straight path towards a lamp post of height H with uniform velocity u. Then the velocity of the edge of the shadow on the ground will be
A. \[\dfrac{{Hu}}{{\left( {H - h} \right)}}\]
B. \[\dfrac{{Hu}}{{\left( {H + h} \right)}}\]
C. \[\dfrac{{H - h}}{{Hu}}\]
D. \[\dfrac{{H + h}}{{Hu}}\]

Answer 1

Hint:The light travels in a straight line and when an obstacle comes in the path of the light then it casts shadow. The distance of the edge of the shadow, the bottom of the lamp post and top of the lamp post makes a right angle triangle.

Formula used:
\[v = \dfrac{{dx}}{{dt}}\]
Here v is the velocity which is mathematically written as the rate of change of position.

Complete step by step solution:

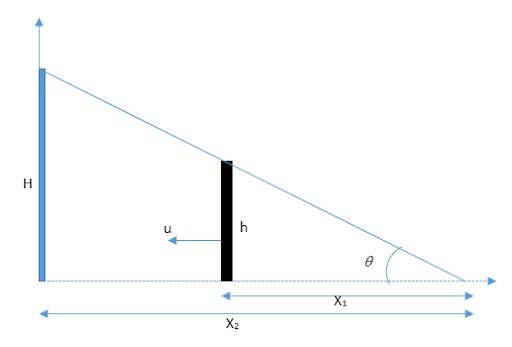
Image: Lamp post and man

Let at any instant of time, the length of the shadow is \[{x_2}\] and the distance of the edge of the shadow from the foot of the man is \[{x_1}\]. The height of the lamp post is given as H and the height of the man is given as h. The distance between the man and the lamp post will be,
\[x = {x_2} - {x_1}\]
It is given that the man is moving towards the lamp post at the uniform velocity u, i.e. the distance between the man and the lamp post is decreasing at the uniform rate of u.
As we know that the velocity is the rate of change of position,
\[ - u = \dfrac{{dx}}{{dt}}\]
\[\Rightarrow - u = \dfrac{{d\left( {{x_2} - {x_1}} \right)}}{{dt}}\]
\[\Rightarrow u = \dfrac{{d{x_1}}}{{dt}} - \dfrac{{d{x_2}}}{{dt}} \ldots \left( i \right)\]
Using congruence of triangle,
\[\tan \theta = \dfrac{H}{{{x_2}}} = \dfrac{h}{{{x_1}}}\]
\[\Rightarrow {x_1} = \dfrac{{h{x_2}}}{H}\]

On differentiating both the sides with respect to time, we get
\[\dfrac{{d{x_1}}}{{dt}} = \dfrac{h}{H}\left( {\dfrac{{d{x_2}}}{{dt}}} \right)\]
Here, \[\dfrac{{d{x_2}}}{{dt}}\] is the velocity of the edge of the shadow, let it be v
\[\dfrac{{d{x_1}}}{{dt}} = \dfrac{{hv}}{H}\]
Putting in the first equation, we get
\[u = \dfrac{{hv}}{H} - v\]
\[\Rightarrow u = v\left( {\dfrac{{h - H}}{H}} \right)\]
\[\therefore v = \dfrac{{Hu}}{{H - H}}\]
So, the edge of the shadow is moving on the ground with uniform speed \[\dfrac{{Hu}}{{H - h}}\].

Therefore, the correct option is A.

Note: Most of the students have confusion between the velocity and speed of an object. Always remember that velocity is a vector quantity and has both velocity and direction but speed is a scalar quantity and has only magnitude.