




Essential Vector Algebra Formulas and Examples for Beginners
Vector Algebra is a central topic in the JEE Main Mathematics syllabus, synthesizing geometric and algebraic reasoning to analyze quantities with both magnitude and direction. Mastery of its concepts is foundational for further studies in geometry, physics, and engineering.
Conceptual Scope and Relevance of Vector Algebra
Vector Algebra studies mathematical entities characterized by both magnitude and direction. Its application ranges from expressing physical phenomena such as displacement and force to providing analytical methods for three-dimensional geometry problems within the JEE Main syllabus.
The chapter encompasses definitions and classifications of vectors, algebraic operations, geometrical representation, scalar and vector products, and their application to problem-solving.
Core Principles and Intuitive Foundation
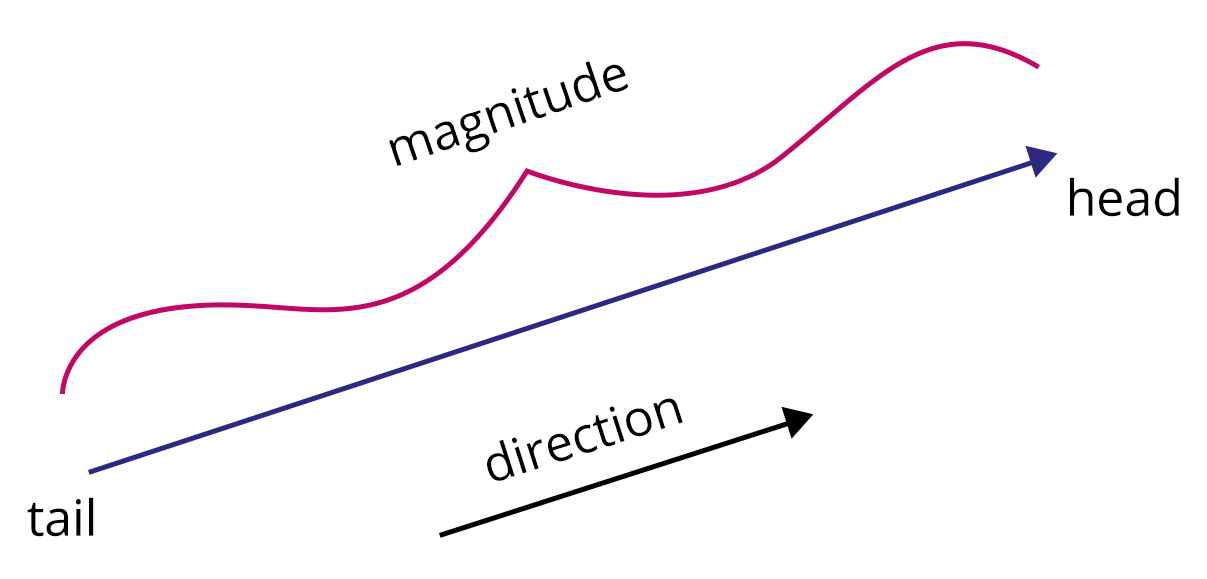
A scalar is a quantity defined solely by magnitude. Examples include length, mass, temperature, and speed.
A vector, in contrast, possesses both magnitude and direction. Instances include displacement, velocity, force, and acceleration. The necessity for vectors arises wherever mere magnitude is insufficient for specifying a property in space.
Vector Notation and Representation Standards
Vectors are denoted using boldface letters such as $\mathbf{a}$, or with an arrow as $\vec{a}$. In component form, a vector in three-dimensional space is expressed as:
$\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$
Here, $a_1$, $a_2$, and $a_3$ are real numbers specifying scalar components along the mutually perpendicular unit vectors $\hat{i}$, $\hat{j}$, and $\hat{k}$ for the x, y, and z axes, respectively.
A position vector identifies the location of a point $P(x, y, z)$ relative to the origin, denoted as $\vec{OP} = x\hat{i} + y\hat{j} + z\hat{k}$.
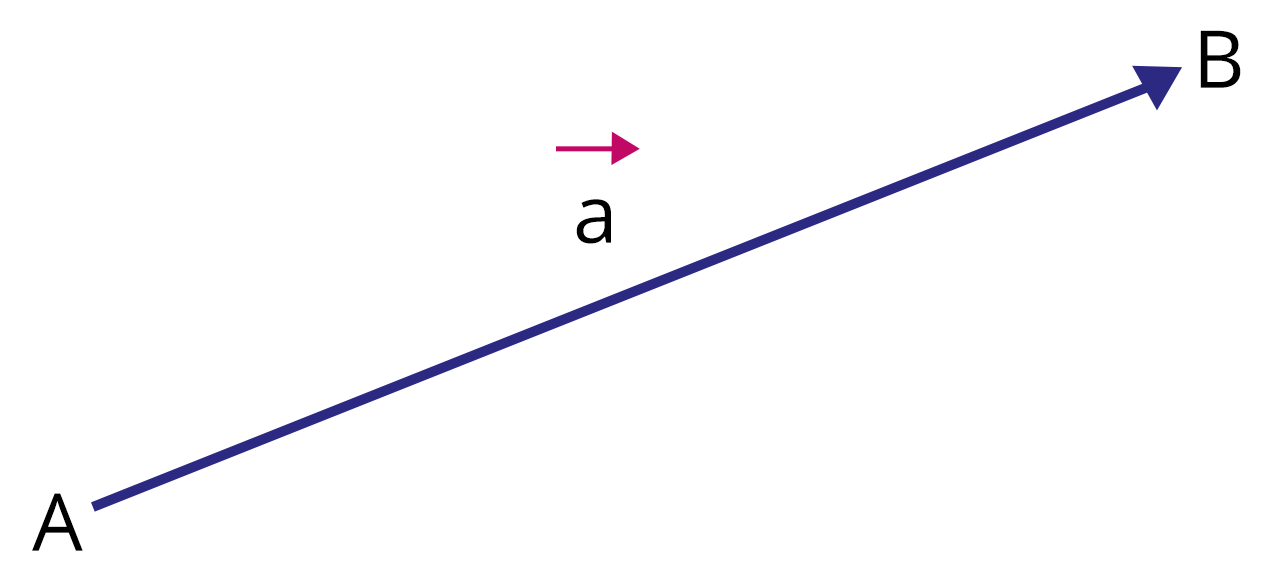
Types of Vectors and Their Properties
- Zero vector
- Unit vector
- Equal vectors
- Negative vector
- Parallel and anti-parallel vectors
- Orthogonal vectors
- Position vector
The zero vector has all components zero and no direction, denoted $\vec{0} = 0\hat{i} + 0\hat{j} + 0\hat{k}$.
A unit vector has magnitude one, indicating direction only; for any non-zero vector $\vec{a}$, its unit vector is $\dfrac{\vec{a}}{|\vec{a}|}$.
Vectors $\vec{a}, \vec{b}$ are equal if their respective components are equal, regardless of starting point.
Parallel vectors have the same direction but may differ in magnitude; anti-parallel vectors have opposite directions.
Orthogonal vectors are perpendicular; their scalar (dot) product is zero.
Magnitude and Direction of a Vector
The magnitude of a vector $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$ is computed as:
$|\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$
For a two-dimensional vector $\vec{a} = a_1\hat{i} + a_2\hat{j}$, the magnitude formula reduces to $|\vec{a}| = \sqrt{a_1^2 + a_2^2}$.
Direction Cosines and Ratios
If a vector forms angles $\alpha, \beta, \gamma$ with the x, y, and z axes, its direction cosines are $\cos\alpha, \cos\beta, \cos\gamma$.
The relation $(\cos^2\alpha + \cos^2\beta + \cos^2\gamma) = 1$ always holds for non-zero vectors.
Direction ratios are any triple $a, b, c$ proportional to the direction cosines.
Vector Operations: Algebraic Structure
- Vector addition
- Vector subtraction
- Multiplication by a scalar
- Scalar (dot) product
- Vector (cross) product
For vectors $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$ and $\vec{b} = b_1\hat{i} + b_2\hat{j} + b_3\hat{k}$:
$\vec{a} + \vec{b} = (a_1 + b_1)\hat{i} + (a_2 + b_2)\hat{j} + (a_3 + b_3)\hat{k}$
$\vec{a} - \vec{b} = (a_1 - b_1)\hat{i} + (a_2 - b_2)\hat{j} + (a_3 - b_3)\hat{k}$
For any scalar $k$, $k\vec{a} = (ka_1)\hat{i} + (ka_2)\hat{j} + (ka_3)\hat{k}$
Scalar (Dot) Product: Definition and Properties
The scalar product of vectors $\vec{a}$ and $\vec{b}$ is:
$\vec{a} \cdot \vec{b} = |\vec{a}|\,|\vec{b}| \cos\theta$
where $\theta$ is the angle between $\vec{a}$ and $\vec{b}$. The result is a scalar.
In component form, $\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 + a_3b_3$
If $\vec{a} \cdot \vec{b} = 0$ and neither vector is zero, they are perpendicular.
Scalar Product of Vectors contains further properties and applications.
Vector (Cross) Product: Definition and Properties
For vectors $\vec{a}$ and $\vec{b}$, their vector product is defined as:
$\vec{a} \times \vec{b} = |\vec{a}|\,|\vec{b}|\,\sin\theta\,\hat{n}$
Here, $\theta$ is the angle between $\vec{a}$ and $\vec{b}$, and $\hat{n}$ is the unit vector perpendicular to the plane of $\vec{a}$ and $\vec{b}$, as determined by the right-hand rule.
In determinant notation:
$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$
First expand the determinant along the first row.
Each term corresponds to a component along $\hat{i}$, $\hat{j}$, or $\hat{k}$, and must be simplified in isolation.
For detailed treatment see Vector Triple Product.
Vector Algebra Formulas: Central Results
- Magnitude: $\sqrt{a_1^2 + a_2^2 + a_3^2}$
- Dot product: $a_1b_1 + a_2b_2 + a_3b_3$
- Cross product: Determinant expansion
- Unit vector: $\dfrac{\vec{a}}{|\vec{a}|}$
Section Formula and Collinearity in Vectors
The vector joining two points $A(x_1, y_1, z_1)$ and $B(x_2, y_2, z_2)$ is:
$\vec{AB} = (x_2 - x_1) \hat{i} + (y_2 - y_1) \hat{j} + (z_2 - z_1) \hat{k}$
A point $P$ divides $AB$ in the ratio $m:n$ (internally):
$\vec{OP} = \dfrac{n\vec{a} + m\vec{b}}{m + n}$
Three points are collinear if their relative vectors are linearly dependent or if the area of the triangle formed by them is zero.
Key Vector Identities and Their Usage
- Distributive and commutative properties
- Vector triple product simplification
- Scalar triple product interpretation
For vectors $\vec{a}$, $\vec{b}$, $\vec{c}$:
$\vec{a} \times (\vec{b} \times \vec{c}) = \vec{b}(\vec{a} \cdot \vec{c}) - \vec{c}(\vec{a} \cdot \vec{b})$
The scalar triple product $[\vec{a}, \vec{b}, \vec{c}] = \vec{a} \cdot (\vec{b} \times \vec{c})$ gives the volume of the parallelepiped formed by the vectors.
Worked Example 1: Magnitude of a Vector
Given $\vec{a} = 5\hat{i} - 3\hat{j} + \hat{k}$.
Use the magnitude formula: $|\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$.
Substitute the values: $|\vec{a}| = \sqrt{(5)^2 + (-3)^2 + (1)^2}$.
Compute each term: $25 + 9 + 1 = 35$.
Take the square root: $|\vec{a}| = \sqrt{35}$.
Worked Example 2: Dot Product of Two Vectors
Let $\vec{a} = 2\hat{i} + 3\hat{j} + \hat{k}$ and $\vec{b} = 5\hat{i} - 2\hat{j} + 3\hat{k}$.
The dot product is $\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 + a_3b_3$.
Substitute values: $2 \times 5 + 3 \times (-2) + 1 \times 3$.
Compute each term: $10 - 6 + 3 = 7$.
The result is $\vec{a} \cdot \vec{b} = 7$.
Worked Example 3: Collinearity and Section Formula
Given $A(1, 2, 3)$, $B(5, 6, 7)$, and $P$ divides $AB$ in the ratio $2:3$ internally.
Write $\vec{OA} = \hat{i} + 2\hat{j} + 3\hat{k}$ and $\vec{OB} = 5\hat{i} + 6\hat{j} + 7\hat{k}$.
Apply the section formula: $\vec{OP} = \dfrac{3\vec{OA} + 2\vec{OB}}{2 + 3}$.
Compute numerator: $3(\hat{i} + 2\hat{j} + 3\hat{k}) + 2(5\hat{i} + 6\hat{j} + 7\hat{k})$.
Expand: $3\hat{i} + 6\hat{j} + 9\hat{k} + 10\hat{i} + 12\hat{j} + 14\hat{k}$.
Sum components: $13\hat{i} + 18\hat{j} + 23\hat{k}$.
Divide by 5: $\vec{OP} = \dfrac{13}{5}\hat{i} + \dfrac{18}{5}\hat{j} + \dfrac{23}{5}\hat{k}$.
Typical JEE Main Patterns in Vector Algebra
- Finding magnitude or direction of a vector
- Verifying collinearity or coplanarity
- Proving perpendicularity or parallelism
- Determinant computation for scalar triple products
- Geometric applications (area, volume)
Common Student Errors in Vector Algebra
- Mistaking direction ratios for direction cosines
- Neglecting to check magnitude when finding unit vectors
- Incorrectly expanding vector cross products
- Mixing up scalar and vector products
Further Practice and Study Resources for JEE Main
Access Vector Algebra Important Questions for targeted practice and Vector Algebra Practice Paper for assessment-style problems.
Refer to Vector Algebra Revision Notes for concise summaries.
Understanding Vector Algebra: A Student’s Guide

 Share
ShareFAQs on Understanding Vector Algebra: A Student’s Guide
1. What is vector algebra?
Vector algebra is a branch of mathematics that deals with quantities having both magnitude and direction, called vectors. Key aspects include:
- Vector addition and subtraction operations
- Scalar and vector multiplication
- Concepts like dot (scalar) product and cross (vector) product
- Use in physics and engineering, matching CBSE syllabus requirements for Class 11 and 12
2. What are the basic properties of vectors?
The main properties of vectors include:
- Magnitude (length of the vector)
- Direction in space
- Can be added or subtracted using the triangle/parallelogram law
- Multiplication by scalars changes magnitude, not direction (except for sign reversal)
- Satisfy commutative, associative laws for addition
3. What is the difference between scalar and vector quantities?
Scalar quantities have only magnitude, while vector quantities have both magnitude and direction.
- Scalars: e.g., mass, temperature, time, speed
- Vectors: e.g., displacement, velocity, force
- Vector operations depend on direction, but scalar operations do not
4. How do you add two vectors geometrically?
Vectors can be added geometrically using the Triangle Law or Parallelogram Law of addition:
- Triangle Law: Place the tail of the second vector at the head of the first; the resultant is from the tail of the first to the head of the second.
- Parallelogram Law: Both vectors start from the same point; the diagonal represents the sum.
5. What is the dot product of two vectors?
The dot product (or scalar product) of two vectors is a scalar quantity given by:
- a · b = |a||b|cosθ, where θ is the angle between a and b.
- It measures how much one vector extends in the direction of another.
- Key properties include commutativity and distributivity over addition.
6. Explain the cross product of two vectors.
The cross product (or vector product) gives a vector perpendicular to both input vectors, with magnitude |a × b| = |a||b|sinθ.
- The direction is determined by the right-hand rule.
- It is not commutative: a × b = -(b × a).
- Applications include finding area of parallelogram defined by two vectors.
7. What is the unit vector? How do you find it?
A unit vector has a magnitude of 1 and indicates direction.
- To find the unit vector in direction of a, use â = a/|a|.
- Unit vectors are denoted by î, j, k̂ for x, y, z axes, respectively.
- Extensively used in resolving vectors in coordinate systems for CBSE and entrance exams.
8. State the parallelogram law of vector addition.
The parallelogram law states that if two vectors are represented by adjacent sides of a parallelogram, their sum is given by the diagonal from their common point.
- Resultant vector formula: R = √(a2 + b2 + 2abcosθ)
- Where a and b are magnitudes, θ is angle between
9. What are collinear vectors?
Collinear vectors are vectors that lie along the same straight line, i.e., their directions are either the same or exactly opposite.
- Mathematically, a and b are collinear if a = k b where k is a scalar.
10. How are vectors used in real-life applications?
Vectors are widely used in real-life applications like:
- Physics: Force, velocity, acceleration
- Engineering: Mechanics, statics, and dynamics
- Navigation: Aircraft and ships use vectors for direction and speed
- Computer graphics: Movement and transformations
11. What is the component form of a vector?
The component form of a vector expresses it in terms of its projections on coordinate axes. For example:
- In 3D: a = a₁î + a₂j + a₃k̂
- a₁, a₂, and a₃ are the scalar components along x, y, z axes respectively
- This form simplifies calculations and resolving vectors for CBSE exams.




















 Watch Video
Watch Video


