Question

With the help of a neat diagram, describe the Geiger-Marsden experiment. What is the mass defect? The photoelectric work function for a metal surface is $2.3{\text{ eV}}{\text{.}}$ If the light of wavelength $6800 A°$ is incident on the surface of metal, find the threshold frequency and incident frequency. Will there be an emission of photoelectric or not? [velocity of light ${\text{c}} = 3 \times {10^8}{\text{ m/s}}$, Planck's constant ${\text{h}} = 6.63 \times {10^{ - 34}}{\text{ Js}}$]

Answer 1

Hint: The Geiger-Marsden experiment is also called the Alpha particle’s scattering experiment in which the alpha particles are incident on the heavy metals like gold, silver, etc. and there happens collision between each alpha particle with one atom of the metal path. The particles can cover the metal path without any dispersion and come out from the opposite surface of the metal path. This incident concludes that the most portion of an atom is vacant.
The mass defect means the difference between the sum of masses of the particles inside the nucleus and the mass of a nucleus.
For the given problem, calculate the incident frequency from the equation of frequency in terms of wavelength. And for calculating the threshold frequency use the equation of the frequency in terms of work function (the minimum energy to photoelectric emission).
For photoelectric emission, the incident frequency must be greater than the threshold frequency.

Formula used:
$\upsilon = \dfrac{c}{\lambda }$
Where, $\upsilon $= the incident frequency
${\text{c}}$= the velocity of light
$\lambda $= the wavelength of the light.
${\upsilon _0} = \dfrac{{{W_0}}}{h}$
Where, ${\upsilon _0}$= the threshold frequency
${W_0}$ = the work function
$h$= Planck's constant.

Complete step by step answer:
First we have to explain the \[{1^{st}}\] Part:
The Geiger-Marsden experiment is also called the Alpha particle’s scattering experiment. The alpha particles that come from an alpha-emitting radioactive source, are incident on the thin plate of heavy metals like gold, silver, etc. The atomic numbers of these types of metals are very high; for Gold the atomic number $Z = 79$ and Silver the atomic number $Z = 47$. Due to a very thin plate, it is assumed that there is a collision between each alpha particle with one atom of the metal path.

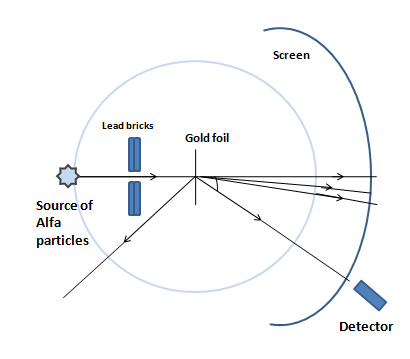
The conclusions and decisions of the experiment are as follow:
1. Most of the particles can cover the metal path without any scattering and come out from the opposite surface of the metal path. This incident concludes that the most portion of an atom is vacant.
2. Some particles scatter a little. In this case, the angle of dispersion is near about ${1^0}$- this is called low angle scattering. This is assumed as the result of the Coulombic attraction between the alpha particle and the electron. This incident concludes that the electrons stay discontinuously in the atom.
3. A very few particles scatter at a large angle. Even sometimes it is near or equals ${90^0}$. Sometimes it is also shown that the particles return fully opposite paths i.e. the scattering angle becomes ${180^0}$. This is called the Large angle scattering. This concludes that the whole charge and almost the whole mass of an atom are centralized – this is called the nucleus.

Mass Defect: The total mass of the nucleons i.e the particles inside the nucleus is less than the mass of the nucleus because a part of the nucleons’ mass converts to the binding energy. The mass defect means the difference between the sum of masses of the particles inside the nucleus and the mass of a nucleus.
\[{2^{nd}}\]Part:
For the given problem, the equation of the frequency of the incident light is,
$\upsilon = \dfrac{c}{\lambda }$
Where, $\upsilon $= the incident frequency
${\text{c}}$= the velocity of light =$3 \times {10^8}{\text{ m/s}}$
$\lambda $= the wavelength of the light = $6800 A°$ = $6800 \times {10^{ - 10}}{\text{ m}}$
$\therefore \upsilon = \dfrac{{3 \times {{10}^8}}}{{6800 \times {{10}^{ - 10}}}}{\text{ Hz}}$
$ \Rightarrow \upsilon = 4.41 \times {10^{14}}{\text{Hz}}$
Hence, the incident frequency is $\upsilon = 4.41 \times {10^{14}}{\text{Hz}}$(Ans).
The threshold frequency is the minimum frequency for emitting photoelectric. The frequency of the threshold frequency is,
${\upsilon _0} = \dfrac{{{W_0}}}{h}$
Where, ${\upsilon _0}$= the threshold frequency
${W_0}$ = the work function= $2.3{\text{ eV}}$= $2.3 \times 1.602 \times {10^{ - 19}}{\text{ J}}$
$h$= Planck's constant.= $6.63 \times {10^{ - 34}}{\text{ Js}}$
$\therefore {\upsilon _0} = \dfrac{{2.3 \times 1.602 \times {{10}^{ - 19}}}}{{6.63 \times {{10}^{ - 34}}}}$
$ \Rightarrow {\upsilon _0} = \dfrac{{3.68 \times {{10}^{ - 19}}}}{{6.63 \times {{10}^{ - 34}}}}$
$ \Rightarrow {\upsilon _0} = 5.55 \times {10^{14}}{\text{ Hz}}$
Hence, the threshold frequency is, ${\upsilon _0} = 5.55 \times {10^{14}}{\text{ Hz}}$ (Ans)
For the photoelectric emission, the incident frequency must be greater than the threshold frequency. Here we see that the threshold frequency is greater than the incident frequency, ${\upsilon _0} > \upsilon $.

Hence the photoelectric emission does not occur.

Note: Threshold frequency: The Threshold frequency of a metal is the minimum frequency of the light for which the photoelectric emission starts.
The work function: The work function of a metal is the minimum energy to start the Photoelectric emission.