Question

Two very long line charges of uniform linear charge density $ + \lambda $ and $ - \lambda $ are placed along the same line with the separation between the nearest ends being $2a$, as shown in the figure. The electric field intensity at a point $O$ is:

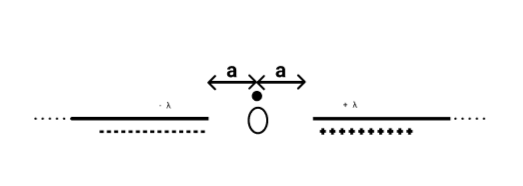
$\left( a \right)$ $0$
$\left( b \right)$ $\dfrac{\lambda }{{\pi {\varepsilon _0}a}}$
$\left( c \right)$ $\dfrac{\lambda }{{2\pi {\varepsilon _0}a}}$
$\left( d \right)$ $\dfrac{\lambda }{{4\pi {\varepsilon _0}a}}$

Answer 1

Hint: In this inquiry, we need to locate the electric field force at the point $O$. So by using the formula for the force on the charged particle due to the section given there. Both will have the same amount of force. The formula will be $dF = kQ\lambda dx/{x^2}$. So by using this we will calculate the force.

Formula used:
Force on the charged particles,
$dF = kQ\lambda dx/{x^2}$
Here,
$dF$, will be a change in the force
$k$, will be the Boltzmann constant
$x$, will be the distance

Complete step by step solution:
So here, most importantly we will ascertain the power of the charged molecule
Therefore, the force on the charged particle is given by
$dF = kQ\lambda dx/{x^2}$
Now on integrating the above equation, we get
$ \Rightarrow F = \int\limits_a^\infty {\dfrac{{kQ\lambda dx}}{{{x^2}}}} $
So, on solving the integration, we will take out the constant part and then put the limit on the rest.
We get
$ \Rightarrow F = kQ\lambda \left[ {\dfrac{{ - 1}}{x}} \right]_a^\infty $
So on solving the limit, we get
$ \Rightarrow F = kQ\lambda \dfrac{1}{a}$
And it can also be written as
$ \Rightarrow F = \dfrac{{kQ\lambda }}{a}$
Since the negative section creates an equal amount of force in the same direction.
So the force for positive and negative will be the same.
Therefore, the total force will be equal to
$ \Rightarrow {F_{Total}} = \dfrac{{kQ\lambda }}{a} + \dfrac{{kQ\lambda }}{a}$
$ \Rightarrow {F_{Total}} = \dfrac{{2kQ\lambda }}{a}$
And also it can be written as
$ \Rightarrow {F_{Total}} = \dfrac{{2k\lambda }}{a}$
And as we know $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$
So the above equation can also be written as
$ \Rightarrow {F_{Total}} = \dfrac{\lambda }{{2\pi {\varepsilon _0}a}}$

So the correct option will be $C$

Notes The course of the Electric line of power for a positive and negative charge. For a positive charge, the electric line moves away and for a negative charge move towards it. At the point when two inverse charges are set shut to one another, they get pulled in. The positive charge Moves toward the electric line of power and goes into a negative charge field which causes the line bend. Two same charges repulse one another.