Question

Two cells of emf 2E and E with internal resistance r1 and r2 respectively are connected in series to an external resistor R (as shown in the circuit). What is the value of R, at which the potential difference across the terminals of the first cell becomes zero?

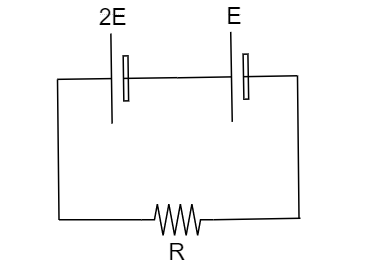
A. \[{r_1} - {r_2}\]
B. \[{r_1} + {r_2}\]
C. \[\dfrac{{{r_1}}}{2} + {r_2}\]
D. \[\dfrac{{{r_1}}}{2} - {r_2}\]

Answer 1

Hint: Before we proceed into the problem, it is important to know the definition of potential difference and internal resistance. Potential difference is defined as the difference of the electrical potential between the two points. The internal resistance opposes the flow of current offered by the cells and batteries themselves resulting in the generation of heat.

Formula Used:
\[i = \dfrac{{3E}}{{R + {r_1} + {r_2}}}\]
Where, E is the emf of the cell, R is the external resistor, $r_1$ and $r_2$ are the internal resistances of the cells.

Complete step by step solution:
Now let us solve the problem step by step considering the definition.

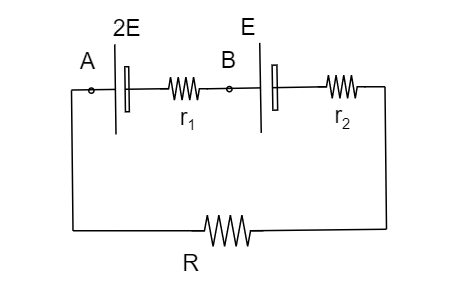
Image: Two cells connected in series with the resistor R.


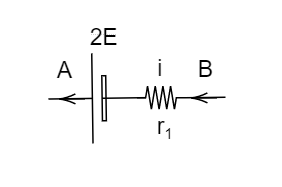
Image: The potential difference across the terminals of the first cell.

By applying the KVL for the given circuit we get,
\[ + 2E - iR - i{r_2} + E - i{r_1} = 0\]
\[\Rightarrow 3E = i({r_1} + {r_2} + R)\]
\[ \Rightarrow i = \dfrac{{3E}}{{R + {r_1} + {r_2}}}\]…….. (1)
In order to find the R value, they have given that the potential difference between point A and B is zero i.e.,

By the circuit we can write the potential difference between the point A and B as,
\[{V_A} - 2E + i{r_1} - {V_B} = 0\]
\[\Rightarrow {V_A} - {V_B} = 2E - i{r_1}\]
\[ \Rightarrow 2E = i{r_1}\]……. (2) Since \[{V_A} - {V_B} = 0\]
Now substituting equation (1) in (2) we get,
\[2E = \dfrac{{3E}}{{R + {r_1} + {r_2}}} \times {r_1}\]
\[\Rightarrow 2R + 2{r_1} + 2{r_2} = 3{r_1}\]
\[\Rightarrow R = \dfrac{{{r_1}}}{2} - {r_2}\]
Therefore, the value of \[R = \dfrac{{{r_1}}}{2} - {r_2}\]

Hence, Option D is the correct answer.

Note: Suppose if two or more cells are connected in parallel having the same emf, then the resultant emf will be equal to the emf of any one of the cells. If the cells are of different emfs, then the resultant emf will be equal to the emf of the cell which is having the greater value of emf.