Question

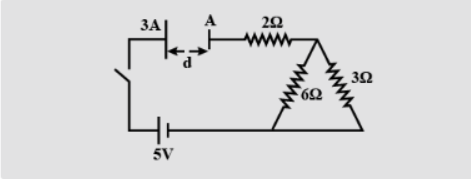
What is the time constant of the C-R growth circuit shown in figure? A, 3A are the areas of the capacitor and d is the distance between them.
(A) $\dfrac{{7{\varepsilon _0}A}}{d}$
(B) $\dfrac{{4{\varepsilon _0}A}}{d}$
(C) $\dfrac{{2{\varepsilon _0}A}}{d}$
(D) $\dfrac{{9{\varepsilon _0}A}}{d}$

Answer 1

Hint: Time constant is the product of capacitance and resistance. C is given by the formula relating area A (which is the common area that is shared by the two plates), distance d between the plates and constant epsilon ε0. Resistance here means the equivalent resistance of the circuit by simplifying parallel and series combinations.

Complete step-by-step solution

In C-R growth circuits the quantity RC is called the time constant as it has the dimension of time.
$t = CR$
C is the capacitance while R is the equivalent resistance of the circuit.
C of the circuit is given by
$C = \dfrac{{{\varepsilon _0}A}}{d}$
Even if the plates are of different areas only the area common is considered hence the capacitance is as above.
Now, we calculate the R
Resistors 3$\Omega $ and 6$\Omega $ are in parallel so
$
  {R_1} = \dfrac{{3 \times 6}}{{3 + 6}} \\
  {R_1} = \dfrac{{18}}{9} \\
  {R_1} = 2\Omega \\
  $
Now $R_1$ is in series with 2$\Omega $
$
  R = {R_1} + 2 \\
  R = 2 + 2 \\
  R = 4\Omega \\
  $
Hence R is equal to 4$\Omega $
Now substitute C and R in the time constant formula
$
  t = CR \\
  t = \dfrac{{{\varepsilon _0}A}}{d} \times 4 \\
  t = \dfrac{{4{\varepsilon _0}A}}{d} \\
  $
Hence the time constant for this circuit is $\dfrac{{4{\varepsilon _0}A}}{d}$.

The correct option is B.

Note: The capacitance value depends linearly on the area of the cross section of the plates, distance between the plates and the medium between the plates while resistance depends linearly on length of the conductor, area and temperature.