
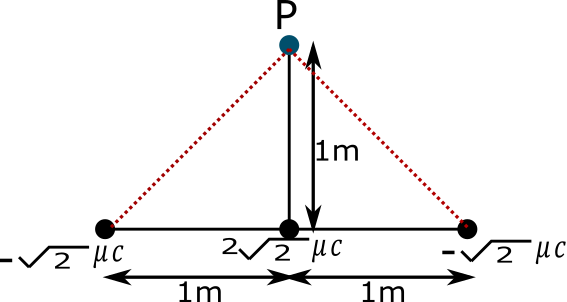
Three charges $ - \sqrt 2 \mu C,2\sqrt 2 \mu C$and $ - \sqrt 2 \mu C$ are arranged as shown. Total electric field intensity at P is:
A) $18 \times {10^3}N/C$
B) $\left( {2\sqrt 2 - 1} \right) \times 9 \times {10^3}N/C$
C) Zero
D) $\left( {2\sqrt 2 + 1} \right) \times 9 \times {10^3}N/C$
Answer
232.8k+ views
Hint: We simply apply here formula for electric field intensity at a point due to a point charge. Here in question three charges are given so we find three electric field intensity on point P. To find the net electric field on point P can be calculated by vector addition of all three electric fields.
Complete step by step solution:
Step 1
First we draw diagram mark electric field direction due to all three charges
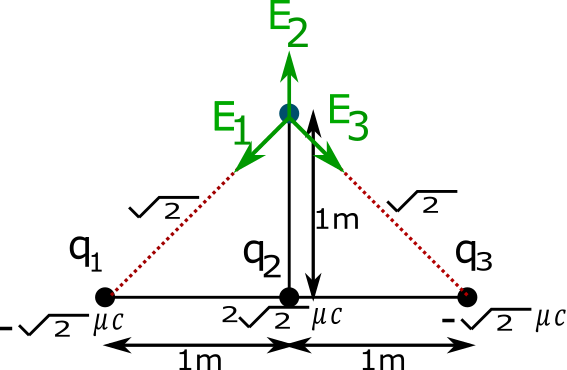
Here charge ${q_1} = - \sqrt 2 \mu C,{q_2} = 2\sqrt 2 \mu C$ and ${q_3} = - \sqrt 2 \mu C$
Electric field due to charge ${q_1}$ is ${E_1}$ toward charge because of negative charge
Electric field due to charge ${q_2}$ is ${E_2}$ away from ${q_2}$ because of positive charge
Electric field due to ${q_3}$ is ${E_3}$ toward ${q_3}$ because of negative charge
Electric field at a point due to a point charge is given by $E = \dfrac{{kq}}{{{r^2}}}$
Here E is the electric field
k is a constant $k = 9 \times {10^9}$
$r$ Is the distance between charge and point
Calculate ${E_1}$
$ \Rightarrow {E_1} = \dfrac{{k{q_1}}}{{{r^2}}}$
Here $r = \sqrt 2 $ from figure
$ \Rightarrow {E_1} = \dfrac{{k\sqrt 2 \times {{10}^{ - 6}}C}}{{{{\left( {\sqrt 2 } \right)}^2}}}$
$ \Rightarrow {E_1} = \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}N/C$ At ${45^\circ }$ from negative y-axis toward negative x-axis
Electric field due to ${q_2}$
$ \Rightarrow {E_2} = \dfrac{{k{q_2}}}{{{r^2}}}$
Here $r = 1m$ given in question
$ \Rightarrow {E_2} = \dfrac{{k \times 2\sqrt 2 \times {{10}^{ - 6}}}}{1}$
$ \Rightarrow {E_2} = k\left( {2\sqrt 2 \times {{10}^{ - 6}}} \right)N/C$ Toward positive y- axis direction
Now ${E_3}$
$ \Rightarrow {E_3} = \dfrac{{k{q_3}}}{{{r^2}}}$
Here $r = \sqrt 2 m$ from diagram
$ \Rightarrow {E_3} = \dfrac{{k \times \sqrt 2 \times {{10}^{ - 6}}}}{{{{\left( {\sqrt 2 } \right)}^2}}}$
$ \Rightarrow {E_3} = \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}N/C$ At ${45^\circ }$ from negative y-axis toward positive x- axis.
Step 2
We assume net electric field due to all three charges is $E$ then
$ \Rightarrow \overrightarrow E = {\overrightarrow E _1} + {\overrightarrow E _2} + {\overrightarrow E _3}$
We make diagram for ${E_1},{E_2}$ and ${E_3}$ with x-y axis
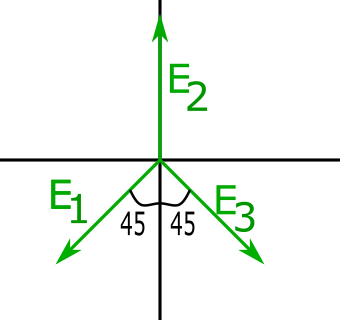
X component for net electric field ${E_x}$
$ \Rightarrow {E_x} = {E_{1x}} + {E_{2x}} + {E_{3x}}$
$ \Rightarrow {E_x} = - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}\sin 45 + 0 + \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}\sin 45$
Solving this
$\therefore {E_x} = 0$
Y component of net electric field ${E_y}$
$ \Rightarrow {E_y} = {E_{1y}} + {E_{2y}} + {E_{3y}}$
$ \Rightarrow {E_y} = \left( { - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}\cos 45} \right) + \left( {k\left( {2\sqrt 2 \times {{10}^{ - 6}}} \right)} \right) + \left( { - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}\cos 45} \right)$
$ \Rightarrow {E_y} = \left( { - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }} \times \dfrac{1}{{\sqrt 2 }}} \right) + \left( {k \times 2\sqrt 2 \times {{10}^{ - 6}}} \right) + \left( { - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }} \times \dfrac{1}{{\sqrt 2 }}} \right)$
Solving this
$ \Rightarrow {E_y} = \left( {k \times {{10}^{ - 6}}} \right)\left( { - \dfrac{1}{2} + 2\sqrt 2 - \dfrac{1}{2}} \right)$
$ \Rightarrow {E_y} = \left( {k \times {{10}^{ - 6}}} \right)\left( {2\sqrt 2 - 1} \right)$
Put the value of constant k
$k = 9 \times {10^9}$
$ \Rightarrow {E_y} = \left( {9 \times {{10}^9} \times {{10}^{ - 6}}} \right)\left( {2\sqrt 2 - 1} \right)$
Solving again
$ \Rightarrow {E_y} = \left( {2\sqrt 2 - 1} \right)\left( {9 \times {{10}^3}} \right)N/C$
So net electric field
$ \Rightarrow E = \sqrt {{{\left( {{E_x}} \right)}^2} + {{\left( {{E_y}} \right)}^2}} $
$ \Rightarrow E = \sqrt {{{\left( 0 \right)}^2} + {{\left[ {\left( {2\sqrt 2 - 1} \right)\left( {9 \times {{10}^3}} \right)} \right]}^2}} $
Hence
$\therefore E = \left( {2\sqrt 2 - 1} \right)\left( {9 \times {{10}^3}} \right)N/C$
So we find net electric field $\left( {2\sqrt 2 - 1} \right) \times 9 \times {10^3}N/C$
Hence option B is correct
Note: In the question we take direction of electric field in positive charge away from the charge and in case of negative charge take toward the charge reason is electric field line
In positive charge electric field lines go away from the positive charge means appears to emit from positive charge and field lines appear to converse at negative charge. So we take the field direction according to this assumption.
Complete step by step solution:
Step 1
First we draw diagram mark electric field direction due to all three charges

Here charge ${q_1} = - \sqrt 2 \mu C,{q_2} = 2\sqrt 2 \mu C$ and ${q_3} = - \sqrt 2 \mu C$
Electric field due to charge ${q_1}$ is ${E_1}$ toward charge because of negative charge
Electric field due to charge ${q_2}$ is ${E_2}$ away from ${q_2}$ because of positive charge
Electric field due to ${q_3}$ is ${E_3}$ toward ${q_3}$ because of negative charge
Electric field at a point due to a point charge is given by $E = \dfrac{{kq}}{{{r^2}}}$
Here E is the electric field
k is a constant $k = 9 \times {10^9}$
$r$ Is the distance between charge and point
Calculate ${E_1}$
$ \Rightarrow {E_1} = \dfrac{{k{q_1}}}{{{r^2}}}$
Here $r = \sqrt 2 $ from figure
$ \Rightarrow {E_1} = \dfrac{{k\sqrt 2 \times {{10}^{ - 6}}C}}{{{{\left( {\sqrt 2 } \right)}^2}}}$
$ \Rightarrow {E_1} = \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}N/C$ At ${45^\circ }$ from negative y-axis toward negative x-axis
Electric field due to ${q_2}$
$ \Rightarrow {E_2} = \dfrac{{k{q_2}}}{{{r^2}}}$
Here $r = 1m$ given in question
$ \Rightarrow {E_2} = \dfrac{{k \times 2\sqrt 2 \times {{10}^{ - 6}}}}{1}$
$ \Rightarrow {E_2} = k\left( {2\sqrt 2 \times {{10}^{ - 6}}} \right)N/C$ Toward positive y- axis direction
Now ${E_3}$
$ \Rightarrow {E_3} = \dfrac{{k{q_3}}}{{{r^2}}}$
Here $r = \sqrt 2 m$ from diagram
$ \Rightarrow {E_3} = \dfrac{{k \times \sqrt 2 \times {{10}^{ - 6}}}}{{{{\left( {\sqrt 2 } \right)}^2}}}$
$ \Rightarrow {E_3} = \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}N/C$ At ${45^\circ }$ from negative y-axis toward positive x- axis.
Step 2
We assume net electric field due to all three charges is $E$ then
$ \Rightarrow \overrightarrow E = {\overrightarrow E _1} + {\overrightarrow E _2} + {\overrightarrow E _3}$
We make diagram for ${E_1},{E_2}$ and ${E_3}$ with x-y axis

X component for net electric field ${E_x}$
$ \Rightarrow {E_x} = {E_{1x}} + {E_{2x}} + {E_{3x}}$
$ \Rightarrow {E_x} = - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}\sin 45 + 0 + \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}\sin 45$
Solving this
$\therefore {E_x} = 0$
Y component of net electric field ${E_y}$
$ \Rightarrow {E_y} = {E_{1y}} + {E_{2y}} + {E_{3y}}$
$ \Rightarrow {E_y} = \left( { - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}\cos 45} \right) + \left( {k\left( {2\sqrt 2 \times {{10}^{ - 6}}} \right)} \right) + \left( { - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }}\cos 45} \right)$
$ \Rightarrow {E_y} = \left( { - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }} \times \dfrac{1}{{\sqrt 2 }}} \right) + \left( {k \times 2\sqrt 2 \times {{10}^{ - 6}}} \right) + \left( { - \dfrac{{k \times {{10}^{ - 6}}}}{{\sqrt 2 }} \times \dfrac{1}{{\sqrt 2 }}} \right)$
Solving this
$ \Rightarrow {E_y} = \left( {k \times {{10}^{ - 6}}} \right)\left( { - \dfrac{1}{2} + 2\sqrt 2 - \dfrac{1}{2}} \right)$
$ \Rightarrow {E_y} = \left( {k \times {{10}^{ - 6}}} \right)\left( {2\sqrt 2 - 1} \right)$
Put the value of constant k
$k = 9 \times {10^9}$
$ \Rightarrow {E_y} = \left( {9 \times {{10}^9} \times {{10}^{ - 6}}} \right)\left( {2\sqrt 2 - 1} \right)$
Solving again
$ \Rightarrow {E_y} = \left( {2\sqrt 2 - 1} \right)\left( {9 \times {{10}^3}} \right)N/C$
So net electric field
$ \Rightarrow E = \sqrt {{{\left( {{E_x}} \right)}^2} + {{\left( {{E_y}} \right)}^2}} $
$ \Rightarrow E = \sqrt {{{\left( 0 \right)}^2} + {{\left[ {\left( {2\sqrt 2 - 1} \right)\left( {9 \times {{10}^3}} \right)} \right]}^2}} $
Hence
$\therefore E = \left( {2\sqrt 2 - 1} \right)\left( {9 \times {{10}^3}} \right)N/C$
So we find net electric field $\left( {2\sqrt 2 - 1} \right) \times 9 \times {10^3}N/C$
Hence option B is correct
Note: In the question we take direction of electric field in positive charge away from the charge and in case of negative charge take toward the charge reason is electric field line
In positive charge electric field lines go away from the positive charge means appears to emit from positive charge and field lines appear to converse at negative charge. So we take the field direction according to this assumption.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26

Understanding the Electric Field of a Uniformly Charged Ring

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Derivation of Equation of Trajectory Explained for Students

Understanding Electromagnetic Waves and Their Importance




