Question

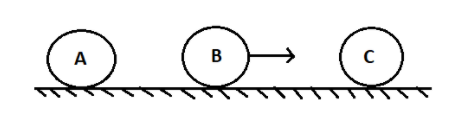
Three balls $A,B$ and $C$$\left( {{m_A} = {m_C} = 4{m_B}} \right)$ are placed on a smooth horizontal surface. The ball $B$ collides with a ball $C$ with an initial velocity $v$ as shown. The total number of collisions between the balls will be (all collisions are elastic)

(A) One
(B) Two
(C) Three
(D) Four

Answer 1

Hint Given that three balls are placed on a smooth surface. Ball $A$ and ball $C$ are of equal mass. They have mass $4$ times that of the ball $B$. It says that the ball $B$ will collide with $C$. We have to find out the number of collisions between the balls. It is given that the collisions are elastic.

Complete Step by step solution
The velocity of the ball $B$ before the collision is given as $v$
After the collision,
Assume that the velocity of $C = {v_1}$
And the velocity of $B = {v_2}$
Hence we can write,
$v = {v_1} + {v_2}$
${v_2}$ will be in the opposite direction of ${v_1}$.
From the equation, $v = {v_1} + {v_2}$
We can write,
${v_1} = v - {v_2}$
We know that the momentum can be written as, $P = mv$
Here applying the conservation of momentum,
${m_B}v = {m_B}{v_2} + {m_C}{v_1}$
Since ${m_C} = 4{m_B}$
Substituting ${m_C} = 4{m_B}$in the above equation we get
${m_B}v = {m_B}{v_2} + 4{m_B}{v_1}$
Eliminating the common terms
We get,
$v = {v_2} + 4{v_1}$………………………………………………(1)
For an elastic collision, the coefficient of restitution is defined as the ratio of the velocity of separation and to the velocity of approach, i.e.
$e = \dfrac{{{v_S}}}{{{v_A}}}$
Where $e$ stands for the coefficient of restitution, ${v_S}$ stands for the velocity of separation, and ${v_A}$stands for the velocity of approach.
Here, we know that the velocity of separation will be, ${v_A} = - \left( {{v_2} - {v_1}} \right) = {v_1} - {v_2}$
The velocity of approach will be, ${v_A} = v$
Hence $e$ can be written as,
$e = \dfrac{{{v_1} - {v_2}}}{v}$
For elastic collision $e = 1$
Hence we can write,
$\dfrac{{{v_1} - {v_2}}}{v} = 1$
$ \Rightarrow {v_1} - {v_2} = v$…………………………………………………………………….(2)
Adding equation (1) and equation (2) we get,
$ {v_2} + 4{v_1} = v +$
  ${v_1} - {v_2} = v$
$ \Rightarrow 5{v_1} = 2v$
Solving the above equation,
${v_1} = \dfrac{2}{5}v$
Substituting the value of ${v_1}$ in equation (2) we get,
$\dfrac{2}{5}v - {v_2} = v$
$ \Rightarrow \dfrac{2}{5}v - v = {v_2}$
From this we get,
${v_2} = - \dfrac{3}{5}v$
Now the ball $C$ will move with a velocity $\dfrac{2}{5}v$ and the ball $B$ will move with a velocity $\dfrac{3}{5}v$ in opposite directions.
The ball $B$ will hit the ball $A$ with a velocity $ - \dfrac{3}{5}v$
Let ${v_3}$be the velocity of the ball $A$
Applying the law of conservation of momentum again, we get
${m_B}\left( { - \dfrac{{3v}}{5}} \right) = - {m_A}{v_3} + {m_B}{\bar v_2}$
We know that ${m_A} = 4{m_B}$
Substituting, we get
${m_B}\left( { - \dfrac{{3v}}{5}} \right) = - 4{m_B}{v_3} + {m_B}{v_2}$
Canceling common terms,
$ - \dfrac{{3v}}{5} = - 4{v_3} + {\bar v_2}$………………………………………………………………………………..(3)
Again considering the coefficient of restitution,
$e = \dfrac{{{v_S}}}{{{v_A}}}$
Where $e$ stands for the coefficient of restitution, ${v_S}$ stands for the velocity of separation, and ${v_A}$ stands for the velocity of approach.
Here, we know that the velocity of separation will be, \[{v_A} = - \left( { - {v_3} - {{\bar v}_2}} \right) = {v_3} + {\bar v_2}\]
The velocity of approach will be, ${v_A} = \dfrac{{3v}}{5}$
$e = \dfrac{{{v_3} + {{\bar v}_2}}}{{\dfrac{{3v}}{5}}}$
Here also the collision is elastic, hence $e = 1$
$\dfrac{{3v}}{5} = {v_3} + {\bar v_2}$……………………………………………………………………………..(4)
Multiplying $4$with equation (4) and adding with equation (3), we get
$ \dfrac{{12v}}{5} = 4{v_3} + 4{{\bar v}_2} +$
  $\dfrac{{ - 3v}}{5} = - 4{v_3} + {{\bar v}_2}$
This will give us,
$\dfrac{{9v}}{5} = 5{\bar v_2}$
From this, we get
${\bar v_2} = \dfrac{{9v}}{{25}}$
Substituting in equation (4)
$\dfrac{{3v}}{5} = {v_3} + \dfrac{{9v}}{{25}}$
From this,
${v_3} = \dfrac{{3v}}{5} - \dfrac{{9v}}{{25}}$
$ \Rightarrow {v_3} = \dfrac{{6v}}{{25}}$
Now the ball $A$ will be moving with a velocity $\dfrac{{6v}}{{25}}$ and the ball $B$ will be moving with a velocity $\dfrac{{9v}}{{25}}$ in the opposite direction. The state will be as shown below

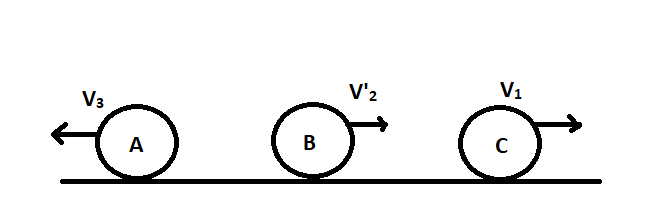
We know that ${\bar v_2} = \dfrac{{9v}}{{25}}$and ${v_1} = \dfrac{{2v}}{5}$
$ \Rightarrow {\bar v_2} \ll {v_1}$
Hence there will not be the third collision. Therefore there will only be two collisions.

The answer is Option (B): Two

Note
In all collisions, the total linear momentum will always be conserved. But the kinetic energy of the system is not always conserved. If the total kinetic energy of a system is conserved after collision such collisions are called elastic collisions and if the total kinetic energy of a system is not conserved after collision then the collision is called an inelastic collision.