
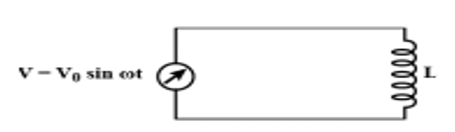
There is no resistance in the inductive circuit. Kirchhoff’s voltage law for the circuit is
A. $V + L\dfrac{{di}}{{dt}} = 0$
B. $V = L\dfrac{{di}}{{dt}}$
C. $V - {L^2}\dfrac{{di}}{{dt}} = 0$
D. None of these
Answer
216.3k+ views
Hint We know that if there is no resistance in an R-L circuit then it is a pure inductor connected to the supply. So, it will be a simple L circuit. At first, we will calculate the voltage drop across the inductor. Then we will apply Kirchhoff laws for finding the appropriate expression.
Complete step by step answer
We know that a RL circuit with no resistance behaves as a purely inductive circuit.
So, we will find the voltage drop across the inductor which is $L\dfrac{{di}}{{dt}}$
Now applying Kirchoff's law for the given circuit with no resistance, we get
$V - L\dfrac{{di}}{{dt}} = 0$
$V = L\dfrac{{di}}{{dt}}$
Where,
V is the voltage drop across the resistor
Therefore, the Kirchoff law for given circuit is $V = L\dfrac{{di}}{{dt}}$
Hence the correct solution is option B
Additional information
In case of time varying input, the inductor opposes the change in current instantaneously. So, the current in the inductor will fall behind and lag with respect to the original. Also, in the pure inductive circuit the phase shift is 90 degrees on considering sinusoidal input.
Note
In the given question no resistance is assumed while writing the Kirchhoff’s law but there is a small resistance of the inductor too which we have neglected in this question.
The above equation is valid for an alternating current as for direct current it behaves as a short circuit and for that current will be zero and simultaneously the voltage drop will be zero.
Complete step by step answer
We know that a RL circuit with no resistance behaves as a purely inductive circuit.
So, we will find the voltage drop across the inductor which is $L\dfrac{{di}}{{dt}}$
Now applying Kirchoff's law for the given circuit with no resistance, we get
$V - L\dfrac{{di}}{{dt}} = 0$
$V = L\dfrac{{di}}{{dt}}$
Where,
V is the voltage drop across the resistor
Therefore, the Kirchoff law for given circuit is $V = L\dfrac{{di}}{{dt}}$
Hence the correct solution is option B
Additional information
In case of time varying input, the inductor opposes the change in current instantaneously. So, the current in the inductor will fall behind and lag with respect to the original. Also, in the pure inductive circuit the phase shift is 90 degrees on considering sinusoidal input.
Note
In the given question no resistance is assumed while writing the Kirchhoff’s law but there is a small resistance of the inductor too which we have neglected in this question.
The above equation is valid for an alternating current as for direct current it behaves as a short circuit and for that current will be zero and simultaneously the voltage drop will be zero.
Recently Updated Pages
Wheatstone Bridge Explained: Working, Formula & Uses

Young’s Double Slit Experiment Derivation Explained

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance

Understanding the Electric Field of a Uniformly Charged Ring

Understanding Average and RMS Value in Electrical Circuits




