
The shortest distance between the line ${\vec{r}}_1=4\vec{i}-3\vec{j}-\vec{k}+\lambda(\vec{i}-4\vec{j}+7\vec{k})$ and ${\vec{r}}_2=\vec{i}-\vec{j}-10\vec{k}+\lambda(2\vec{i}-3\vec{j}+8\vec{k})$ is –
A. 3
B. 1
C. 2
D. 0
Answer
232.8k+ views
Hint: To determine the shortest distance between any two lines we must determine the shortest distance between any two points on both lines. There are different types of lines: parallel lines, intersecting lines, and skew lines.
1. Parallel lines
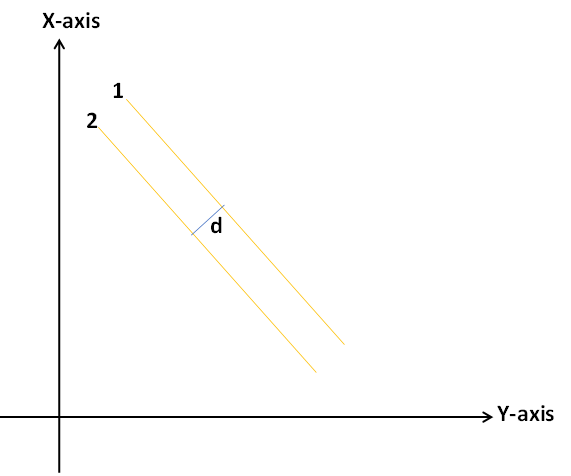
All distance between parallel lines will be the same/constant.
2. Intersecting lines
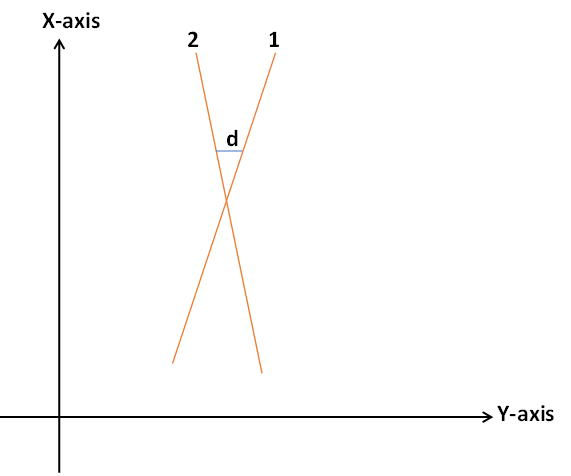
The shortest distance between the intersecting lines will be zero.
3. Skew lines

Formula used: The formula to determine the distance between the lines $r_1=a_1+\lambda b_1$ and $r_2=a_2+\lambda b_2$ are –
$d=\left\bracevert\dfrac{(a_2-a_1).(b_1\times b_2)}{\left|b_1\times b_2\right|}\right\bracevert$
Complete step by step solution: Given, the equations of the lines are –
${\vec{r}}_1=4\vec{i}-3\vec{j}-\vec{k}+\lambda(\vec{i}-4\vec{j}+7\vec{k})$ ---------- (i)
${\vec{r}}_2=\vec{i}-\vec{j}-10\vec{k}+\lambda(2\vec{i}-3\vec{j}+8\vec{k})$ ---------- (ii)
We know that to determine the shortest distance between the lines-
$r_1=a_1+\lambda b_1$ and $r_2=a_2+\lambda b_2$
$d=\left\bracevert\dfrac{(a_2-a_1).(b_1\times b_2)}{\left|b_1\times b_2\right|}\right\bracevert$
On comparing the equations (i) and (ii) with equations of lines $[ r_1=a_1+\lambda b_1 ]$ and $[ r_2=a_2+\lambda b_2 ]$ respectively
$a_1=4\vec{i}-3\vec{j}-\vec{k}$ and $a_2=\vec{i}-\vec{j}-10\vec{k}$
$b_1=\vec{i}-4\vec{j}+7\vec{k}$ and $b_2=2\vec{i}-3\vec{j}+8\vec{k}$
$a_2-a_1=\vec{i}-\vec{j}-10\vec{k}-(4\vec{i}-3\vec{j}-\vec{k})$
$a_2-a_1=\vec{i}-\vec{j}-10\vec{k}-4\vec{i}+3\vec{j}+\vec{k}$
$a_2-a_1=-3\vec{i}+2\vec{j}-9\vec{k}$
${b}_{1}\times{b}_{2}=\vec{{i}}[(-{4})\times{8}-{7}\times(-{3})]-j[(7×2)-(8×1)]-k[(-3)×1-2×(-4)]$
${b}_{1}\times{b}_{2}=\vec{{i}}[(-{32})-(-{21})]+j[(14)-(8)]-k[(-3)-(-8)]$
${b}_{1}\times{b}_{2}=\vec{{i}}[(-{32})+({21})]+j[(14)-(8)]-k[(-3)-(-8)]$
${b}_{1}\times{b}_{2}=-{11}\vec{{i}}+{6}\vec{{j}}+{5}\vec{{k}}$
$(a_2-a_1).(b_1\times b_2)=(-3\vec{i}+2\vec{j}-9\vec{k}).(-{11}\vec{{i}}+{6}\vec{{j}}+{5}\vec{{k}})$
$(a_2-a_1).(b_1\times b_2)=(-3).(-{11})(\vec{{i}}.\vec{i})+(2.{6})(\vec{{j}}.\vec{j})+(-9).(-{5})(\vec{{k}}.\vec{k})$
As we know that $(\vec{{i}}.\vec{i})=(\vec{{j}}.\vec{j})=(\vec{{k}}.\vec{k})=1$
$(a_2-a_1).(b_1\times b_2)={33}+12-45$
$a_2-a_1).(b_1\times b_2)={45}-45$
$(a_2-a_1).(b_1\times b_2)={0}$
$\left|b_1\times b_2\right|=\sqrt{{(-11)}^2+{(6)}^2+{(5)}^2}$
$\left|b_1\times b_2\right|=\sqrt{121+36+25}$
$\left|b_1\times b_2\right|=\sqrt{182}$
$d=\left|\frac{(a_2-a_1).(b_1\times b_2)}{\left|b_1\times b_2\right|}\right|=\frac{0}{\sqrt{182}}=0$
Hence the shortest distance between the line [ ${\vec{r}}_1=4\vec{i}-3\vec{j}-\vec{k}+\lambda(\vec{i}-4\vec{j}+7\vec{k}) ]$ and $[ {\vec{r}}_2=\vec{i}-\vec{j}-10\vec{k}+\lambda(2\vec{i}-3\vec{j}+8\vec{k}) ]$ is 0.
Thus, Option (D) is correct.
Note: The direction ratios (a, b, c) are components of vector with respect to x-axis, y-axis, and z-axis respectively and direction cosines (l, m, n) are the angle subtended by the line with x-axis, y-axis, and z-axis respectively.
1. Parallel lines

All distance between parallel lines will be the same/constant.
2. Intersecting lines
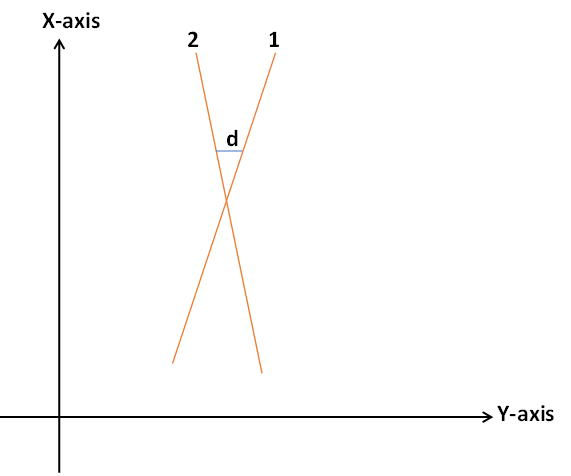
The shortest distance between the intersecting lines will be zero.
3. Skew lines

Formula used: The formula to determine the distance between the lines $r_1=a_1+\lambda b_1$ and $r_2=a_2+\lambda b_2$ are –
$d=\left\bracevert\dfrac{(a_2-a_1).(b_1\times b_2)}{\left|b_1\times b_2\right|}\right\bracevert$
Complete step by step solution: Given, the equations of the lines are –
${\vec{r}}_1=4\vec{i}-3\vec{j}-\vec{k}+\lambda(\vec{i}-4\vec{j}+7\vec{k})$ ---------- (i)
${\vec{r}}_2=\vec{i}-\vec{j}-10\vec{k}+\lambda(2\vec{i}-3\vec{j}+8\vec{k})$ ---------- (ii)
We know that to determine the shortest distance between the lines-
$r_1=a_1+\lambda b_1$ and $r_2=a_2+\lambda b_2$
$d=\left\bracevert\dfrac{(a_2-a_1).(b_1\times b_2)}{\left|b_1\times b_2\right|}\right\bracevert$
On comparing the equations (i) and (ii) with equations of lines $[ r_1=a_1+\lambda b_1 ]$ and $[ r_2=a_2+\lambda b_2 ]$ respectively
$a_1=4\vec{i}-3\vec{j}-\vec{k}$ and $a_2=\vec{i}-\vec{j}-10\vec{k}$
$b_1=\vec{i}-4\vec{j}+7\vec{k}$ and $b_2=2\vec{i}-3\vec{j}+8\vec{k}$
$a_2-a_1=\vec{i}-\vec{j}-10\vec{k}-(4\vec{i}-3\vec{j}-\vec{k})$
$a_2-a_1=\vec{i}-\vec{j}-10\vec{k}-4\vec{i}+3\vec{j}+\vec{k}$
$a_2-a_1=-3\vec{i}+2\vec{j}-9\vec{k}$
${b}_{1}\times{b}_{2}=\vec{{i}}[(-{4})\times{8}-{7}\times(-{3})]-j[(7×2)-(8×1)]-k[(-3)×1-2×(-4)]$
${b}_{1}\times{b}_{2}=\vec{{i}}[(-{32})-(-{21})]+j[(14)-(8)]-k[(-3)-(-8)]$
${b}_{1}\times{b}_{2}=\vec{{i}}[(-{32})+({21})]+j[(14)-(8)]-k[(-3)-(-8)]$
${b}_{1}\times{b}_{2}=-{11}\vec{{i}}+{6}\vec{{j}}+{5}\vec{{k}}$
$(a_2-a_1).(b_1\times b_2)=(-3\vec{i}+2\vec{j}-9\vec{k}).(-{11}\vec{{i}}+{6}\vec{{j}}+{5}\vec{{k}})$
$(a_2-a_1).(b_1\times b_2)=(-3).(-{11})(\vec{{i}}.\vec{i})+(2.{6})(\vec{{j}}.\vec{j})+(-9).(-{5})(\vec{{k}}.\vec{k})$
As we know that $(\vec{{i}}.\vec{i})=(\vec{{j}}.\vec{j})=(\vec{{k}}.\vec{k})=1$
$(a_2-a_1).(b_1\times b_2)={33}+12-45$
$a_2-a_1).(b_1\times b_2)={45}-45$
$(a_2-a_1).(b_1\times b_2)={0}$
$\left|b_1\times b_2\right|=\sqrt{{(-11)}^2+{(6)}^2+{(5)}^2}$
$\left|b_1\times b_2\right|=\sqrt{121+36+25}$
$\left|b_1\times b_2\right|=\sqrt{182}$
$d=\left|\frac{(a_2-a_1).(b_1\times b_2)}{\left|b_1\times b_2\right|}\right|=\frac{0}{\sqrt{182}}=0$
Hence the shortest distance between the line [ ${\vec{r}}_1=4\vec{i}-3\vec{j}-\vec{k}+\lambda(\vec{i}-4\vec{j}+7\vec{k}) ]$ and $[ {\vec{r}}_2=\vec{i}-\vec{j}-10\vec{k}+\lambda(2\vec{i}-3\vec{j}+8\vec{k}) ]$ is 0.
Thus, Option (D) is correct.
Note: The direction ratios (a, b, c) are components of vector with respect to x-axis, y-axis, and z-axis respectively and direction cosines (l, m, n) are the angle subtended by the line with x-axis, y-axis, and z-axis respectively.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding the Electric Field of a Uniformly Charged Ring

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Derivation of Equation of Trajectory Explained for Students

Understanding Electromagnetic Waves and Their Importance

Understanding How a Current Loop Acts as a Magnetic Dipole

Understanding Average and RMS Value in Electrical Circuits




