Question

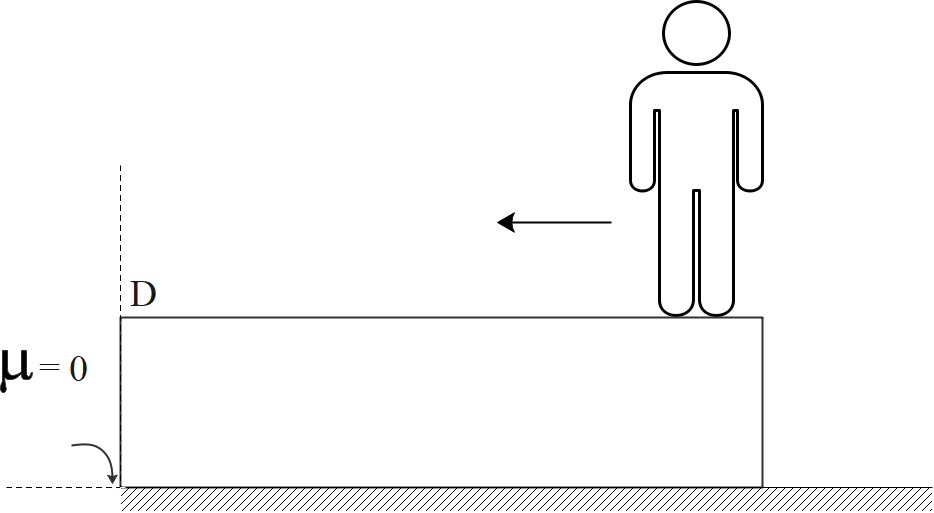
The frequency of sound detected by detector D, after man jumps off plank is:


(A) $\dfrac{{332}}{{324}}{f_0}$
(B) $\dfrac{{330}}{{322}}{f_0}$
(C) $\dfrac{{328}}{{336}}{f_0}$
(D) $\dfrac{{330}}{{338}}{f_0}$

Answer 1

Hint: The question is centred around the concepts of Doppler Effect which is the increase or decrease in the frequency of light, sound or other waves when the source or observer moves towards each other or away from each other. Some effects that we see in our daily lives are the noticeable pitch in a passing siren, and the red shift in image of celestial bodies as seen by astronomers.

Complete step by step answer:
Let v be the speed with which the plank moves backwards. Therefore, the speed with which the man moves forward is (8-v), the relative speed of both the bodies being 8m/s.
Since, the system is frictionless, i.e., no external force acts on the system in the horizontal direction, the net velocity of the centre of mass of that system remains constant i.e., equal to 0.
\[
  \therefore {\text{ }}\dfrac{{{{\text{m}}_{\text{1}}}{{\text{v}}_{\text{1}}}{\text{ + }}{{\text{m}}_{\text{2}}}{{\text{v}}_{\text{2}}}}}{{{{\text{m}}_{\text{1}}}{\text{ + }}{{\text{m}}_{\text{2}}}}} = 0 \\
   \Rightarrow {\text{ }}\dfrac{{{\text{50}}\left( {8 - {\text{v}}} \right){\text{ + 150}}\left( {\text{v}} \right)}}{{50 + 150}} = 0 \\
   \Rightarrow {\text{ v = 2 m/s towards right}} \\
 \]
Therefore, speed is ${\text{8 m/s }} - {\text{ 2 m/s = 6 m/s towards left}}$.
When the man jumps off the plank, they recede each other in the opposite direction with same speeds.
According to the Doppler Effect, frequency heard by the detector ${\text{ = }}{{\text{f}}_{\text{0}}}\left( {\dfrac{{{\text{c}} - {{\text{v}}_{\text{o}}}}}{{{\text{v}} - {{\text{v}}_{\text{s}}}}}} \right){\text{ = }}{{\text{f}}_{\text{0}}}\left( {\dfrac{{330 - 2}}{{{\text{330 + }}6}}} \right) = \dfrac{{328}}{{336}}{{\text{f}}_{\text{0}}}$

Hence, the correct answer is option C.

Note: For the calculation of Doppler effect, relative speeds are the most important. The speed with which either of them moves towards or away from the other, or the speed with which both of them moves towards or away from each other, determines the frequency of sound according to the Doppler effect.