Question

The figure shows a circuit that contains four identical resistors with resistance R = 2.0 Ω. Two identical inductors with inductance L = 2.0 mH and an ideal battery with emf E = 9.V. The current ‘i’ just after the switch ‘s’ is closed will be


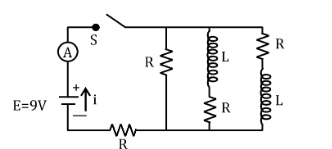
A. 9A
B. 3.0 A
C. 2.25 A
D. 3.37 A

Answer 1

Hint: At the instant when the switch is closed, it is derived from basic concepts that the inductor behaves like a resistance of infinite value. Based on the above inference the circuit can be redrawn to analyse its behavior just as the switch is closed.

Formula used:
Basic form of Ohm’s Law assuming ideal conditions is written below
 \[V = I \times R\] ………… (1)
Where, V= Voltage across a resistive element in Volts
              I= Current through the resistive element in Amperes
             R= Resistance offered to the flow of current by the element in Ohms


Complete answer:
Here, after redrawing the circuit to represent the state just after the switch is closed. The inductor is assumed to be a resistance of infinite value.
   
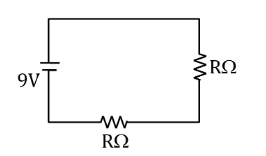
Image: Circuit just after switch is closed
Data given:
R= 2.0 ohm
L= 2mH (milli Henry)
E=9 V
Putting the values given above and using Ohm’s Law (1) for the circuit drawn above (2), we can write ,
\[\dfrac{V}{I} = R\]
\[R = \]\[2 + 2 = 4\] Ohm
Here, The equivalent resistance is added because the resistances given are in series.
\[I = \dfrac{V}{R} = \dfrac{9}{4} = 2.25\] Amperes
Hence, the current just after the switch is closed is 2.25 Amperes.

The correct answer is C.

Note: This problem deals with transient state analysis. During the transient state there is a change in the variables or process, but this stage is temporary and finally the system reaches a steady state. As the circuit is in a transient state just after the switch is closed, the inductor behaves as open circuit. Students often make a common mistake to solve the given question. They used a second loop to solve. Here we need to use the first loop.