Question

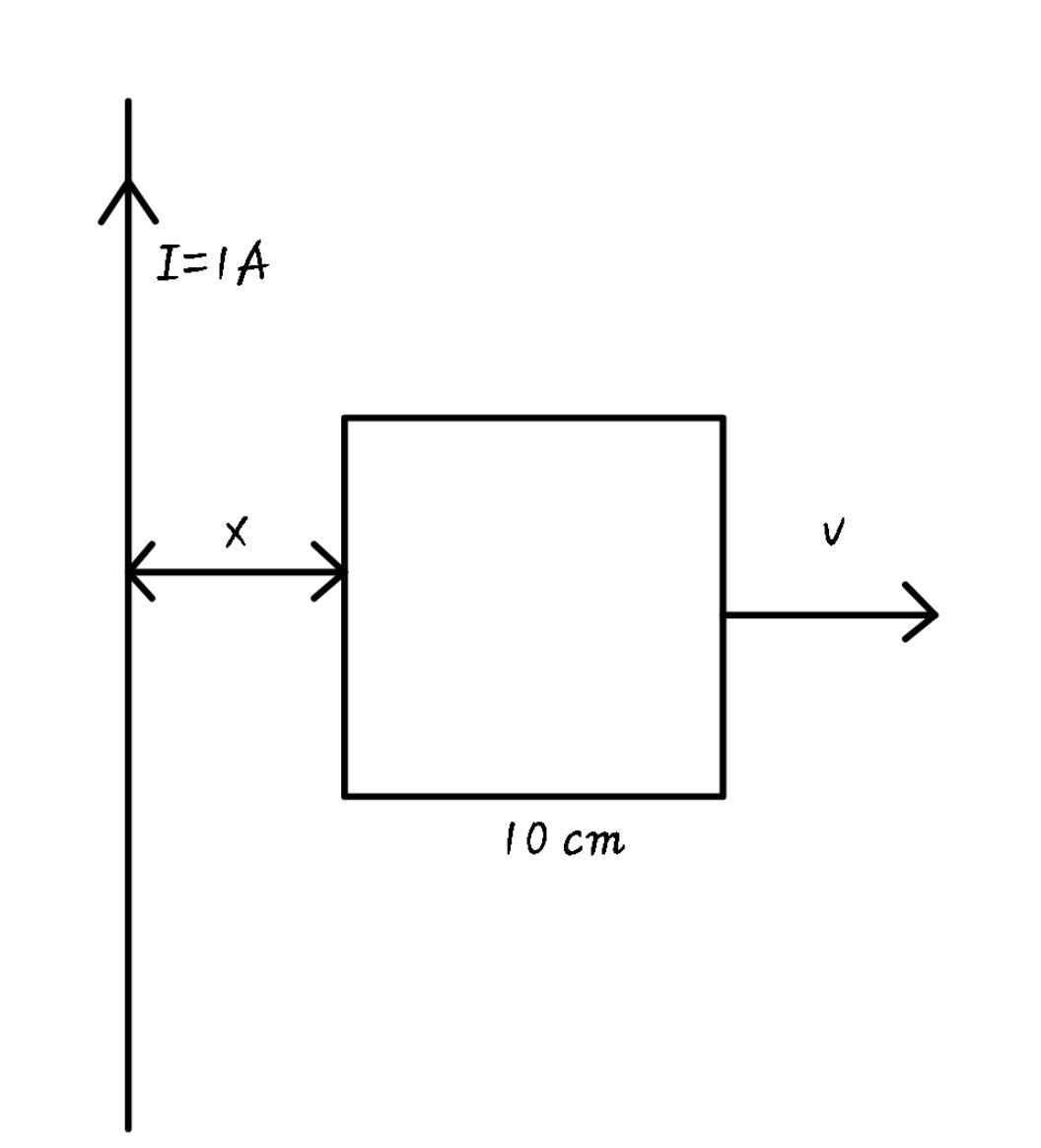
A square frame of side $10\text{ cm}$ and a long straight wire carrying current 1A are in the plane of the paper. Starting from close to the drive, the frame moves towards the right with a constant speed of $10\text{ m}{{\text{s}}^{-1}}$ (see figure). The e.m.f induced in the frame at the time the left arm is at $\text{x}=10\text{ cm}$ from the wire is:

(A) $\text{2 }\!\!\mu\!\!\text{ V}$
(B) $\text{1 }\!\!\mu\!\!\text{ V}$
(C) $\text{0}\cdot 75\text{ }\!\!\mu\!\!\text{ V}$
(D) $\text{0}\cdot \text{5 }\!\!\mu\!\!\text{ V}$

Answer 1

Hint Here we will use the concept of motional emf. when an electric conductor is moved in presence of magnetic field, an emf is induced in it (according to Lenz law), that emf is called motional emf.
It is given by expression:
$\text{e}=\left( \overrightarrow{\text{v}}\times \overrightarrow{\text{B}} \right)\times \overrightarrow{\text{l}}$
Where, v is the velocity with which it is moved.
    $\overrightarrow{\text{B}}$ is magnetic field
    $\text{ }\overrightarrow{\text{l}}$is length of the conductor

Complete step by step solution
Mentioned emf is given by expression
    $\text{e}=\left( \overrightarrow{\text{v}}\times \overrightarrow{\text{B}} \right)\times \overrightarrow{\text{l}}$…. (1)
In this situation, if we apply the right hand thumb rule to calculate the direction of the magnetic field. It comes out to be directed into the paper (as shown in figure).
Therefore, here the magnetic field, velocity and length of the conductor are perpendicular to each other.
$\therefore $ 1 becomes,
    $\text{e}=\left( \text{vB sin 90}{}^\circ \right)\times \text{l}$ (v and B are perpendicular to each other)
    $\begin{align}
  & =\text{vBl cos 0}{}^\circ \\
 & \text{=vBl} \\
\end{align}$ [Resultant of cross product of v and B is parallel to l]
For arms CD and AB of the square frame, l is parallel to v. as (i) is also called a scalar triple product.
And if two quantities are in parallel, then it turns out to be zero.
$\therefore $No emotional emf is there.
Also,
Magnetic field reached at AD is more than magnetic field at arm BC
$\therefore $${{\text{B}}_{\text{AD}}}>{{\text{B}}_{\text{BC}}}$
Using Lenz law, one can find that, direction of current in the coil is in clockwise direction. (As magnetic field is directed inward)
    Emf induced in arm AD,${{\text{e}}_{1}}={{\text{B}}_{\text{AD}}}\text{vl}$
    Emf induces in arm BC,${{\text{e}}_{2}}={{\text{B}}_{\text{BC}}}\text{vl}$
    Resultant emf,${{\text{e}}_{\text{net}}}=\text{vl}\left( {{\text{B}}_{1}}-{{\text{B}}_{2}} \right)$…. (2)
    $\begin{align}
  & {{\text{B}}_{1}}=\frac{{{\text{ }\!\!\mu\!\!\text{ }}_{0}}\text{I}}{2\text{ }\!\!\pi\!\!\text{ }{{\text{r}}_{\text{1}}}}=\frac{{{\text{ }\!\!\mu\!\!\text{ }}_{0}}\times 1}{2\text{ }\!\!\pi\!\!\text{ }\times \text{1}{{\text{0}}^{-1}}} \\
 & {{\text{B}}_{2}}=\frac{{{\text{ }\!\!\mu\!\!\text{ }}_{0}}\text{I}}{2\text{ }\!\!\pi\!\!\text{ }{{\text{r}}_{2}}}=\frac{{{\text{ }\!\!\mu\!\!\text{ }}_{0}}\times 1}{2\text{ }\!\!\pi\!\!\text{ }\times \text{1}{{\text{0}}^{-1}}\times 2} \\
\end{align}$
(Where${{\text{r}}_{1}}\And {{\text{r}}_{2}}$ are distance of arm AD and BC from current carrying conductor respectively]
Substituting all values in equation (2), we get
    \[\begin{align}
  & {{\text{e}}_{\text{net}}}=10\times 10\times {{10}^{-2}}\left[ \frac{{{\text{ }\!\!\mu\!\!\text{ }}_{0}}}{2\text{ }\!\!\pi\!\!\text{ }\times \text{1}{{\text{0}}^{-1}}}-\frac{{{\text{ }\!\!\mu\!\!\text{ }}_{0}}}{2\text{ }\!\!\pi\!\!\text{ }\times \text{1}{{\text{0}}^{-1}}\times 2} \right] \\
 & \text{ }=\frac{{{\text{ }\!\!\mu\!\!\text{ }}_{0}}\times 10}{2\text{ }\!\!\pi\!\!\text{ }}\left[ 1-\frac{1}{2} \right] \\
 & \text{ }=\frac{{{\text{ }\!\!\mu\!\!\text{ }}_{\text{0}}}}{\text{4 }\!\!\pi\!\!\text{ }}\times 10 \\
\end{align}\]
    \[\begin{align}
  & \text{ }={{10}^{-7}}\times 10 \\
 & \text{ }={{10}^{-6}} \\
 & \text{ }=1\text{ }\!\!\mu\!\!\text{ V} \\
\end{align}\]

Therefore, the option (B) is correct.

Note Here we have used the formula of magnetic field due to a straight current carrying wire,
    \[\text{B}=\frac{{{\text{ }\!\!\mu\!\!\text{ }}_{0}}}{4\text{ }\!\!\pi\!\!\text{ }}=\frac{2\text{I}}{\text{r}}\] Where, r is distance of observation point from conductor and I, is current moving in the conductor.
Remember following points about Lenz law:
According to Lenz’s law: The polarity of the induced emf is such that it tends to produce induced current in such a direction that it opposes the change in magnetic flux that produced it.
The ($-$) live sign in given equation e$=\left( - \right)\left( \text{d}\Phi \text{/dt} \right)$ tells about the direction
According to Lenz’s law the direction of the induced current will be such that it opposes the change in the magnetic flux.