Question

The electrostatic charge system is shown in figure, find:

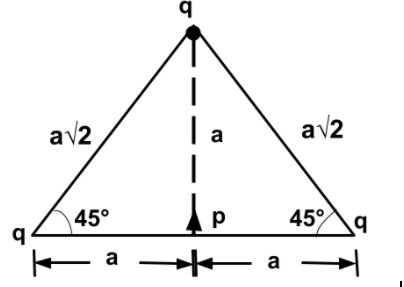
A) The net force on electric dipole, and
B) Electrostatic energy of the system

Answer 1

Hint: To find the net force on electric dipole due to up, left and right charges and find their addition. Then, by using the expression of electric potential energy for the interaction of all three charges we will get the electrostatic energy of the system.

Complete step by step solution:
A) Let the force exerted by the upper charge on dipole be ${F_1}$, force exerted by the left charge be ${F_2}$ and force exerted by the right charge on dipole be ${F_3}$.
Force exerted by the upper charge on the dipole is –
\[{F_1} = - \dfrac{1}{{2\pi {\varepsilon _0}}}\dfrac{{pq}}{{{a^3}}} \cdots \left( 1 \right)\]
where, $p$ is the dipole moment, $q$ is the charge and $a$ is the distance between them.
Similarly, force exerted by the left charge on dipole –
\[{F_2} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{pq}}{{{a^3}}} \cdots \left( 2 \right)\]
Now, force exerted by the right charge on dipole –
\[{F_3} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{pq}}{{{a^3}}} \cdots \left( 3 \right)\]
Now, finding the net force on the dipole due to all charges. So, we have to add equation $\left( 1 \right),\left( 2 \right)\& \left( 3 \right)$ -
$\
{F_{net}} = {F_1} + {F_2} + {F_3} \\
\Rightarrow {F_{net}} = - \dfrac{1}{{2\pi {\varepsilon _0}}}\dfrac{{pq}}{{{a^3}}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{pq}}{{{a^3}}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{pq}}{{{a^3}}} \\
\Rightarrow {F_{net}} = - \dfrac{1}{{2\pi {\varepsilon _0}}}\dfrac{{pq}}{{{a^3}}} + \dfrac{1}{{2\pi {\varepsilon _0}}}\dfrac{{pq}}{{{a^3}}} \\
\Rightarrow {F_{net}} = 0 \\
\ $
Hence, net force acting on the dipole is zero.

B) The total electrostatic energy of the system is the interaction of all three charges with each other and the interaction with the dipole.
Therefore, -
$U = 2\left( {\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q^2}}}{{\sqrt 2 a}}} \right) + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q^2}}}{{2a}}$
Now, $ - P.{E_{up}} - P.E - P.{E_{right}}$
We know that electric fields produced by left and right charges are perpendicular to P.
So, $P.{E_{left}} = P.{E_{right}} = 0$
We know that, potential energy of dipole in uniform electric field is, $U = - pE\cos \theta $
Therefore,
$\
   - P.{E_{up}} = - P.\left( {\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{a^2}}}} \right)\cos \pi \\
   \Rightarrow \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{qp}}{{{a^2}}} \\
\ $
Now, putting the values in the above equation –
$U = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q^2}}}{{2a}}\left[ {2\sqrt 2 + 1} \right]$
Hence, we got the total energy of the dipole due to interaction of all the charges.

Note: When the point is between two equal and opposite charges the electric potential becomes zero but electric field is not equal to zero. When Electric field produced by left and right charges is perpendicular to P so, we know that, $\cos {90^ \circ } = 0$. Hence, the electric field becomes zero.