Question

The diagram shows two resistors X and Y connected in parallel across a voltage source. Choose the correct statement from the option given below:

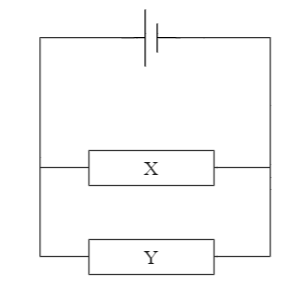
(A) The combined resistance is equal to the sum of the resistance
(B) The current at every point in the circuit is the same
(C) The current from the source is equal to the sum of the currents in X and Y
(D) The sum of the potential difference across X and across Y is equal to the potential difference across the voltage source.

Answer 1

Hint: Any amount of charge that enters a system is equal to the amount that goes out of it. This basic principle is also well-known as one of Kirchhoff’s laws and is used to determine the current and/or voltage at a node.

Complete step by step answer:
We are provided with two resistors X and Y connected in parallel. We know that the equivalent resistance in the case of a parallel connection is given by:
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
Hence, this rules out the first option as the sum is not equal to the linear sum of two resistances.
We also know that Kirchoff’s law states that the amount of current entering a node is equal to the amount of current leaving the node. So, if ${I_1}$ current enters X and ${I_2}$ current enters Y through the node beside them, the total current that should be going into the node is:
$I = {I_1} + {I_2}$
This implies that option B is wrong and option C is correct. But what about the option D? We know that the potential difference across a component does not get distributed along node lines as the current does.
So, option D is wrong.

Hence, option C is the right answer.

Note: The voltage drop across a component does not get divided in the same way as the current does. This is because the potential difference depends directly on both the current and the resistance of the component. So, even if the current remains constant across two components from the same node, the different resistances would cause a different potential drop.