Question

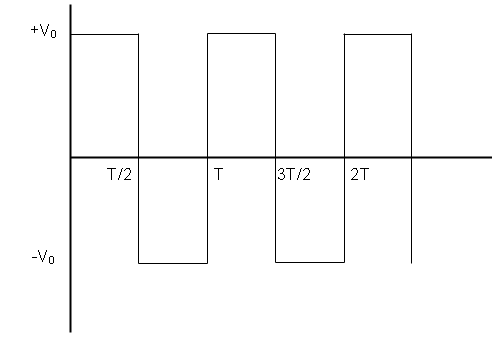
The average and RMS value of voltage for square waves shown in the fig. having a peak value ${V_0}$ are:

(A) $\dfrac{{{V_0}}}{{\sqrt 2 }},\sqrt 2 {V_0}$
(B) $\sqrt 2 {V_0},\dfrac{{{V_0}}}{{\sqrt 2 }}$
(C) ${V_0},{V_0}$
(D) Zero, ${V_0}$

Answer 1

Hint: In this solution, we will use the formula of average and RMS value. We only need to consider one cycle of the voltage to calculate the average and RMS value.

Complete step by step answer:
In the graph given to us, we want to calculate the average and RMS value of voltage.
The average amplitude is the mathematical “mean” of all a waveform’s points over the period of one cycle. It can be mathematically calculated as:
${V_{avg}} = \dfrac{1}{T}\int {{V_0}dt} $
We can see that the waveform of the voltage starts a cycle at $t = 0$ and ends the cycle at $t = T$. To calculate the integral of the wave function given to us, we need to break the integral down into regions where the voltage has constant values. So, we can write
${V_{avg}} = \dfrac{1}{T}\left( {\int\limits_{t = 0}^{t = T/2} {{V_0}dt + } \int\limits_{t = T/2}^{t = T} { - {V_0}dt} } \right)$
The ${V_0}$ term can be taken out of the integral since it is constant. The integral can then be simplified to
${V_{avg}} = \dfrac{{{V_0}}}{T}\left( {\dfrac{T}{2} + \dfrac{T}{2} - T} \right)$
$ \Rightarrow {V_{avg}} = 0$
Hence the average voltage will be zero.
Now, The RMS value stands for Root Mean Square value. It is a way of expressing an AC quantity of voltage or current in terms functionally equivalent to DC. It can be mathematically calculated as
${V_{RMS}} = \sqrt {\dfrac{1}{T}\int\limits_{t = 0}^T {{V^2}dt} } $
The integral can be broken into two parts as
${V_{RMS}} = \sqrt {\dfrac{1}{T}\left( {\int\limits_{t = 0}^{t = T/2} {V_0^2dt} + \int\limits_{t = T/2}^{t = T} {V_0^2dt} } \right)} $
The integral can be simplified as
${V_{RMS}} = \sqrt {\dfrac{{{V_0}^2}}{T}T} $
Or,
${V_{RMS}} = {V_0}$

Hence the correct choice is option (D).

Note: While calculating the average and the RMS value, we must not forget the $1/T$ term outside the integral. We can also find the average value graphically as zero since the area of the graph for one time period is the same in the positive and negative regime and as such, the average value will be zero.