Question

The area bounded by the curve \[y = {\sin ^{ - 1}}x\] and the line \[x = 0,y = \dfrac{\pi }{2}\] is
A. 1
B. 2
C. \[\pi \]
D. \[2\pi \]

Answer 1

Hint: In this case, we gave to relate the \[\sin x\] and \[{\sin ^{ - 1}}x\] graphs by the \[\sin x\] range, i.e. 0,1 and also create a neat graphic to calculate the area of the bounded region based on the given curves. The area enclosed by lines, \[x = a,{\rm{ }}x = b,y = f\left( x \right)\] is equal to \[ = \int\limits_a^b {f(x)dx} \] where (b> a)

Formula Used: To determine the area of the shaded region, we use the formula
\[ = \int\limits_a^b {f(x)dx} \]

Complete step by step solution: We are provided in the question that the curve is
\[y = {\sin ^{ - 1}}x\]
And the line will be as mentioned below,
\[x = 0,y = \dfrac{\pi }{2}\]
Now, we are to determine the area bounded by the curve
\[y = {\sin ^{ - 1}}x\]
For that, we have to make a graph for the given data, we have


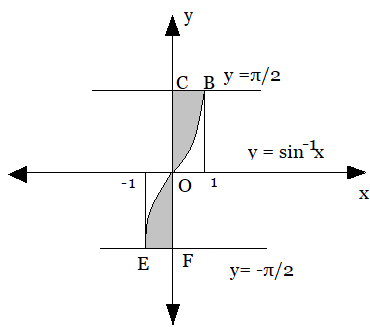
Now, let us determine the area of the shaded region from the above graph.
\[y = {\sin ^{ - 1}}x\]
Because the graph is symmetrical about the origin, the bounded area is given by
\[A = 2\int\limits_0^1 {{{\sin }^{ - 1}}xdx} \]
Now, on solving the limit from the above equation, we obtain
\[ = 2\left[ {\left| {x{{\sin }^{ - 1}}x} \right|_0^1 - \int_0^1 x \dfrac{1}{{\sqrt {1 - {x^2}} }}dx} \right]\]
On solving the other limit by replacing the limit value to the corresponding places, we get
\[ = 2\left[ {\left| {\dfrac{\pi }{2} + \sqrt {1 - {x^2}} } \right|_0^1} \right]\]
Now, we have to substitute the limit values in the place of x to determine the value, we have
\[ = \pi - 2\]
Now, let us determine the area of the shaded region, we have
\[ = \mid Ar(OABC) + Ar(ODEF) - A\mid \]
On substituting the values from the given diagram, we get
\[ = \left| {\dfrac{\pi }{2} \times 1 + \dfrac{\pi }{2} \times 1 - \pi + 2} \right|\]
We can write the above expression in less complicated form as below,
\[ = \dfrac{\pi }{2} + \dfrac{\pi }{2} - \pi + 2\]
We have been already known that the value of \[\pi \] is \[3.141593\] and therefore \[\dfrac{\pi }{2}\] is \[1.570796\]
So on replacing, we get
\[1.570796 + 1.570796 - 3.141593 + 2\]
Now, we have to simplify the above expression by adding/subtraction we get
\[ = 0 + 2\]
On further simplification, we get
\[ = 2\]
Therefore, the area bounded by the curve \[y = {\sin ^{ - 1}}x\] and the line \[x = 0,y = \dfrac{\pi }{2}\] is \[2\] units

Option ‘B’ is correct

Note: When confronted with such situations, the crucial concept to remember is to always recollect the basic integration formulas such as \[\int {\sin xdx = - \cos x + c,\int {\cos xdx = \sin x + c} } \] where c is some arbitrary integration constant and the area under the curve using the integration approach indicated above.