Question

The angle of elevation of the top of a hill from a point on the horizontal plane passing through the foot of the hill is found to be ${{45}^{\circ }}$. After walking a distance of $80$ meters towards the top, up a slope inclined at an angle of ${{30}^{\circ }}$ to the horizontal plane, the angle of elevation of the top of the hill becomes $75^{\circ}$. Then the height of the hill (in meters) is:

Answer 1

Hint: In order to solve the question we will first make the diagram by using all the information given in the question then we will introduce some of the variables such as x,y,z and h and after that we will use trigonometric identities of cos x , sin x and tan x so that we can find the height of the hill (in meters)

Formula Used:
$\left[ \cos x=\dfrac{Base}{Hypotenuse} \right]$
$\left[ \sin x=\dfrac{Perpendicular}{Hypotenuse} \right]$
$\left[ \tan x=\dfrac{Perpendicular}{Base} \right]$

Complete step by step solution:
Let the height of the hill be $h$ meters.

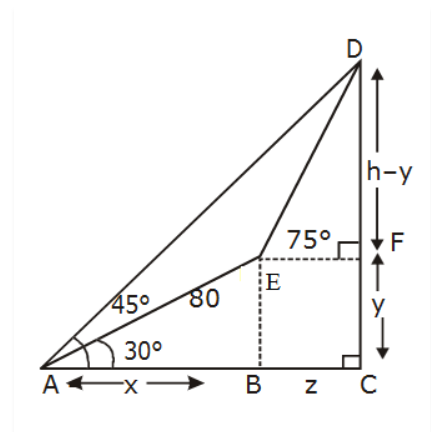
Image: Right angled triangle
In $\Delta ABE$, we have
$\cos {{30}^{\circ }}=\dfrac{x}{80}$ $\left[ \cos x=\dfrac{Base}{Hypotenuse} \right]$
$\Rightarrow x=80\times \cos {{30}^{\circ }}$
We know that $\cos {{30}^{\circ }}=\dfrac{\sqrt{3}}{2}$, we get
$\Rightarrow x=80\times \dfrac{\sqrt{3}}{2}$
$\Rightarrow x=40\sqrt{3}\,m$
And,
$\sin {{30}^{\circ }}=\dfrac{y}{80}$ $\left[ \sin x=\dfrac{Perpendicular}{Hypotenuse} \right]$
$\Rightarrow y=80\times \sin {{30}^{\circ }}$
We know that $\sin {{30}^{\circ }}=\dfrac{1}{2}$, we get
$\Rightarrow y=80\times \dfrac{1}{2}$
$\Rightarrow y=40\,m$
In $\Delta ADC$, we have
$\tan {{45}^{\circ }}=\dfrac{h}{x+z}$ $\left[ \tan x=\dfrac{Perpendicular}{Base} \right]$
We know that $\tan {{45}^{\circ }}=1$. Therefore, we get
$\Rightarrow 1=\dfrac{h}{x+z}$
$\Rightarrow h=x+z$
Now substitute the value of $x$
$\Rightarrow h=40\sqrt{3}+z\,\,\,\,........\left( i \right)$
In $\Delta EDF$, we have
$\tan {{75}^{\circ }}=\dfrac{h-y}{z}$ $\left[ \tan x=\dfrac{Perpendicular}{Base} \right]$
We know that $\tan {{75}^{\circ }}=2+\sqrt{3}$. Therefore, we get
$\Rightarrow 2+\sqrt{3}=\dfrac{h-y}{z}$
$\Rightarrow z=\dfrac{h-y}{2+\sqrt{3}}$
Now, substitute the value of $y$
$\Rightarrow z=\dfrac{h-40}{2+\sqrt{3}}$
Now, put the value of $z$ in equation $\left( i \right)$
$\Rightarrow h=40\sqrt{3}+\dfrac{h-40}{2+\sqrt{3}}$
Take L.C.M.
$\Rightarrow h=\dfrac{40\sqrt{3}\left( 2+\sqrt{3} \right)+h-40}{2+\sqrt{3}}$
$\Rightarrow h=\dfrac{80\sqrt{3}+120+h-40}{2+\sqrt{3}}$
On cross multiplication, we get
$\Rightarrow h\left( 2+\sqrt{3} \right)=80\sqrt{3}+80+h$
$\Rightarrow h\left( 2+\sqrt{3} \right)-h=80\sqrt{3}+80$
On subtraction of like terms, we get
$\Rightarrow 2h+\sqrt{3}h-h=80\sqrt{3}+80$
On subtraction, we get
$\Rightarrow h+\sqrt{3}h=80+80\sqrt{3}$
$\Rightarrow h\left( 1+\sqrt{3} \right)=80\left( 1+\sqrt{3} \right)$
On canceling the common terms, we get
$\Rightarrow h=80\,m$
Hence, the height of the hill is $80\,m$.

Note: The difference between an angle of depression and an angle of elevation is that the latter refers to the angle between the horizontal and the object. Applying the idea of trigonometric functions is made easier by realising that the structure and the lighthouse form right angled triangles. It is required to be familiar with the trigonometric table of the tan function.