Question

Six x’s are to be placed in the square of the figure given below such that each row contains at least one X. Then find the number of ways this can be done.
A.18
B.22
C.26
D.30

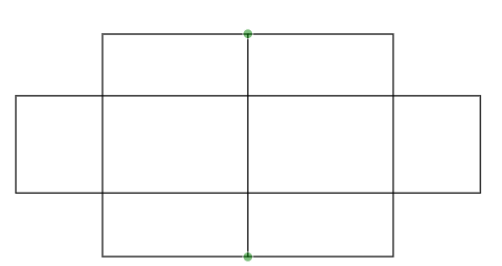
Images: Boxes of three row

Answer 1

Hints First obtain the conditions by which the x’s can be put in 3 rows. Then use combination to obtain the number of ways x can be placed in the first row, then similarly find the result for the second and third rows. Then add all the obtained number of ways to conclude the final result.

Formula used
\[{}^n{C_r} = \dfrac{{n!}}{{r!\left( {n - r} \right)!}}\] .

Complete step by step solution
In the given figure, the first row contains 2 boxes, the second row contains 4 boxes and the third row contains 2 boxes.
There are 4 condition to put six x’s at a time in a row:
(1,4,1), (1,3,2), (2,3,1), (2,2,2).
In the first condition, the x’s can be placed in \[{}^2{C_1} \times {}^4{C_4} \times {}^2{C_1}\] ways,
that is in \[2 \times 1 \times 2 = 4\] ways.
In the second condition, the x’s can be placed in \[{}^2{C_1} \times {}^4{C_3} \times {}^2{C_2}\] ways,
that is in \[2 \times 4 \times 1 = 8\] ways.
In the third condition, the x’s can be placed in \[{}^2{C_2} \times {}^4{C_3} \times {}^2{C_1}\] ways,
that is in \[1 \times 4 \times 2 = 8\] ways.
In the fourth condition, the x’s can be placed in \[{}^2{C_2} \times {}^4{C_2} \times {}^2{C_2}\] ways,
that is in \[1 \times 6 \times 1 = 6\] ways.
Therefore, the total number of ways is 4+8+8+6=26.
The correct option is C.

Note The students can rearrange the order of the condition and calculate on their own, it is not mandatory to follow the order of the condition. Sometimes students get confused and calculate only the first condition and wrote 4 as an answer but that is not correct, we need to calculate the four conditions to obtain the required answer 26.