Question

Show that the points \[( - 4, - 7),( - 1,2),(8,5)\]and \[(5, - 4)\] taken in order are the vertices of a rhombus. Also find its area.

Answer 1

Hint: We find the lengths of each side of the quadrilateral formed by joining the given four vertices taken in order. Use the formula to calculate the distance between two distinct points. Check if the quadrilateral is rhombus using the definition of rhombus. Calculate the length of diagonals using the end points and use the formula for the area of rhombus.
$\Rightarrow$ A rhombus is a quadrilateral having all sides of equal length. Opposite sides of a rhombus are parallel and opposite angles of a rhombus are equal. The diagonals of rhombus are not equal to each other.
$\Rightarrow$ If rhombus has diagonals \[{d_1},{d_2}\]then its area is given by \[\dfrac{1}{2} \times {d_1} \times {d_2}\].
$\Rightarrow$ Distance between two points \[({x_1},{y_1}),({x_2},{y_2})\]is given by \[\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} \].

Complete step by step answer:
We are given four points \[( - 4, - 7),( - 1,2),(8,5)\] and \[(5, - 4)\]
Let us denote each point using a point A, B, C and D respectively.
Then quadrilateral ABCD has vertices \[A( - 4, - 7),B( - 1,2),C(8,5),D(5, - 4)\]

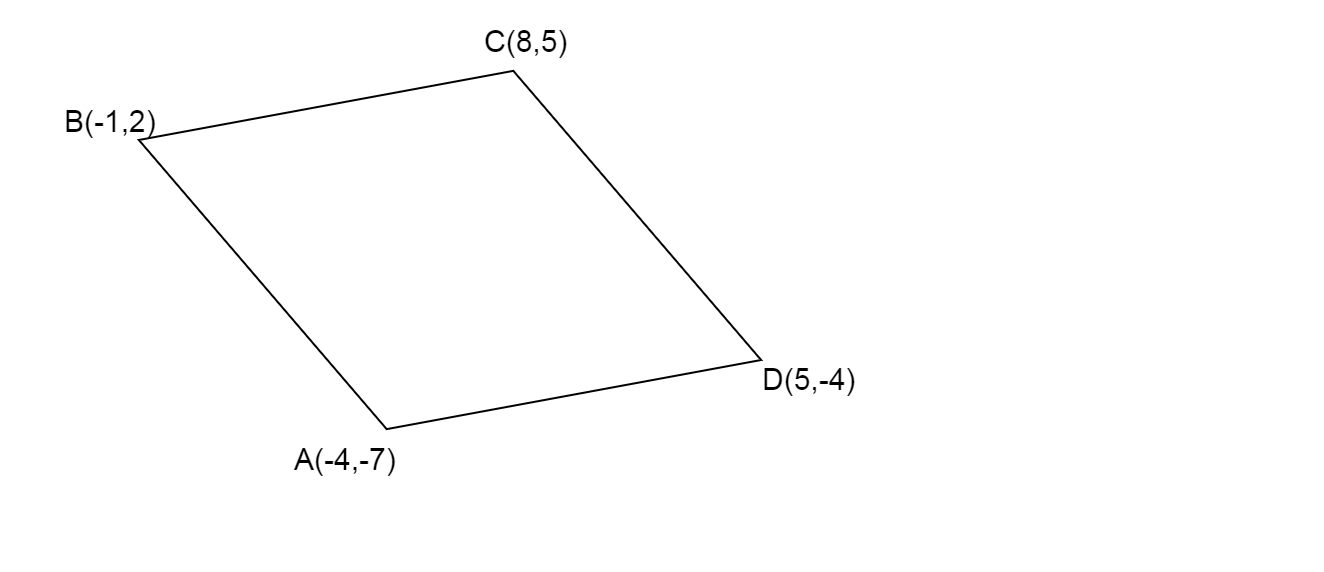
Calculate distance between two points separately for each side of the quadrilateral.
Side AB:
Points joining the side AB are\[A( - 4, - 7),B( - 1,2)\]
Since the distance between two points \[({x_1},{y_1}),({x_2},{y_2})\]is given by \[\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} \]
Here \[{x_1} = - 4,{y_1} = - 7,{x_2} = - 1,{y_2} = 2\]
\[ \Rightarrow AB = \sqrt {{{( - 1 - ( - 4))}^2} + {{(2 - ( - 7))}^2}} \]
Multiply the negative signs together to give positive sign
\[ \Rightarrow AB = \sqrt {{{( - 1 + 4)}^2} + {{(2 + 7)}^2}} \]
\[ \Rightarrow AB = \sqrt {{{(3)}^2} + {{(9)}^2}} \]
Write the square of values inside the under root
\[ \Rightarrow AB = \sqrt {9 + 81} \]
\[ \Rightarrow AB = \sqrt {90} \] units……………...… (1)
Side BC:
Points joining the side BC are\[B( - 1,2),C(8,5)\]
Since the distance between two points \[({x_1},{y_1}),({x_2},{y_2})\]is given by \[\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} \]
Here \[{x_1} = - 1,{y_1} = 2,{x_2} = 8,{y_2} = 5\]
\[ \Rightarrow BC = \sqrt {{{(8 - ( - 1))}^2} + {{(5 - (2))}^2}} \]
Multiply the negative signs together to give positive sign
\[ \Rightarrow BC = \sqrt {{{(8 + 1)}^2} + {{(5 - 2)}^2}} \]
\[ \Rightarrow BC = \sqrt {{{(9)}^2} + {{(3)}^2}} \]
Write the square of values inside the under root
\[ \Rightarrow BC = \sqrt {81 + 9} \]
\[ \Rightarrow BC = \sqrt {90} \] units………..… (2)
Side CD:
Points joining the side CD are\[C(8,5),D(5, - 4)\]
Since the distance between two points \[({x_1},{y_1}),({x_2},{y_2})\] is given by \[\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} \]
Here \[{x_1} = 8,{y_1} = 5,{x_2} = 5,{y_2} = - 4\]
\[ \Rightarrow CD = \sqrt {{{(5 - 8)}^2} + {{( - 4 - 5)}^2}} \]
\[ \Rightarrow CD = \sqrt {{{(3)}^2} + {{( - 9)}^2}} \]
Write the square of values inside the under root
\[ \Rightarrow CD = \sqrt {9 + 81} \]
\[ \Rightarrow CD = \sqrt {90} \] units………….… (3)
Side DA:
Points joining the side DA are \[D(5, - 4), A( - 4, - 7)\]
Since the distance between two points \[({x_1},{y_1}),({x_2},{y_2})\]is given by \[\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} \]
Here \[{x_1} = 5,{y_1} = - 4,{x_2} = - 4,{y_2} = - 7\]
\[ \Rightarrow DA = \sqrt {{{( - 4 - 5)}^2} + {{( - 7 - ( - 4))}^2}} \]
Multiply the negative signs together to give positive sign
\[ \Rightarrow DA = \sqrt {{{( - 4 - 5)}^2} + {{( - 7 + 4)}^2}} \]
\[ \Rightarrow DA = \sqrt {{{( - 9)}^2} + {{( - 3)}^2}} \]
Write the square of values inside the under root
\[ \Rightarrow DA = \sqrt {81 + 9} \]
\[ \Rightarrow DA = \sqrt {90} \] units………….… (4)
From equations (1), (2), (3) and (4)
\[AB = BC = CD = DA = \sqrt {90} \]units
Now we find the length of diagonals.

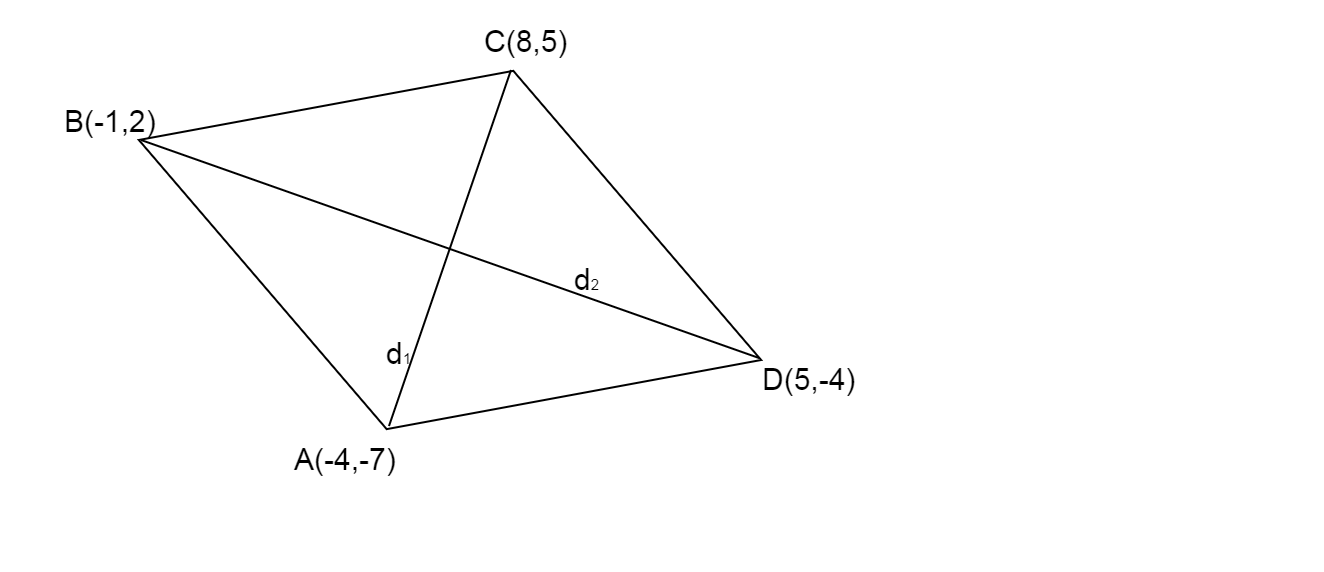
Diagonals of rhombus ABCD are AC and BD
Diagonal AC:
Points joining the side AC are \[A( - 4, - 7), C(8,5)\]
Since the distance between two points \[({x_1},{y_1}),({x_2},{y_2})\] is given by \[\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} \]
Here \[{x_1} = - 4,{y_1} = - 7,{x_2} = 8,{y_2} = 5\]
\[ \Rightarrow AC = \sqrt {{{(8 - ( - 4))}^2} + {{(5 - ( - 7))}^2}} \]
Multiply the negative signs together to give positive sign
\[ \Rightarrow AC = \sqrt {{{(8 + 4)}^2} + {{(5 + 7)}^2}} \]
\[ \Rightarrow AC = \sqrt {{{(12)}^2} + {{(12)}^2}} \]
Write the square of values inside the under root
\[ \Rightarrow AC = \sqrt {144 + 144} \]
\[ \Rightarrow AC = \sqrt {2 \times {{(12)}^2}} \]
Cancel square power by square root
\[ \Rightarrow AC = 12\sqrt 2 \] units………………..… (5)
Diagonal BD:
Points joining the side BD are \[B( - 1,2), D(5, - 4)\]
Since the distance between two points \[({x_1},{y_1}),({x_2},{y_2})\]is given by \[\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} \]
Here \[{x_1} = - 1,{y_1} = 2,{x_2} = 5,{y_2} = - 4\]
\[ \Rightarrow BD = \sqrt {{{(5 - ( - 1))}^2} + {{( - 4 - 2)}^2}} \]
Multiply the negative signs together to give positive sign
\[ \Rightarrow BD = \sqrt {{{(5 + 1)}^2} + {{( - 4 - 2)}^2}} \]
\[ \Rightarrow BD = \sqrt {{{(6)}^2} + {{(6)}^2}} \]
Write the square of values inside the under root
\[ \Rightarrow BD = \sqrt {36 + 36} \]
\[ \Rightarrow BD = \sqrt {2 \times 36} \]
\[ \Rightarrow BD = \sqrt {2 \times {{(6)}^2}} \]
Cancel square power by square root
\[ \Rightarrow BD = 6\sqrt 2 \] units……………..… (6)
Since the diagonals AC and BD are of different lengths and all sides are of equal length, then from the definition of Rhombus, ABCD is a rhombus.
Hence proved.
Substitute the values of AC and BD from equations (5) and (6) in the formula of area of rhombus.
Area of rhombus is given by the formula \[\dfrac{1}{2} \times {d_1} \times {d_2}\] where \[{d_1}\] and \[{d_2}\] are diagonals of rhombus.
In rhombus ABCD, AC and BD are diagonals.
\[ \Rightarrow \]Area\[ = \dfrac{1}{2} \times AC \times BD\]
\[ \Rightarrow \]Area\[ = \dfrac{1}{2} \times 12\sqrt 2 \times 6\sqrt 2 \]
We write \[\sqrt 2 \times \sqrt 2 = {(\sqrt 2 )^2} = 2\] in the RHS of the equation.
\[ \Rightarrow \]Area\[ = \dfrac{1}{2} \times 2 \times 12 \times 6\]
Cancel out the same factors from numerator and denominator.
\[ \Rightarrow \]Area\[ = 72\] square units.

\[\therefore \]Area of rhombus is 72 square units.

Note: Many students confuse a rhombus with a square. A square and rhombus both have all their sides of equal length but in square the length of diagonals is equal to each other and in rhombus the length of diagonals is never equal to each other.
Students are likely to get confused while calculating the value of sides as they make mistakes with negative signs of vertices, it is advised to write the x and y coordinate inside the bracket first and then solve. Also, write the SI unit of area along with the area and SI unit of length along with length of sides.