Question

Question: A survey shows that 61%, 46% and 29% of the people watched 3 idiots, Raajneeti and Avatar respectively. 25% people watched exactly two of the three movies and 3% watches none. What percentage of people watched all the three movies?
A) \[39\% \]
B) \[11\% \]
C) \[14\% \]
D) \[7\% \]

Answer 1

Hint: In this question, we have to find what percentage of people watched all three movie. In order to find this concept of Venn diagram is used. Draw intersection of Venn diagram and then by using diagram find solution.

Formula used: In this question we are going to use the Venn diagram. This diagram give the relation between various set and their subset.

Complete step by step solution:

Draw a Venn-diagram taking three intersecting sets 3 idiots, Rajneeti and Avatar. After intersection even regions will be developed.

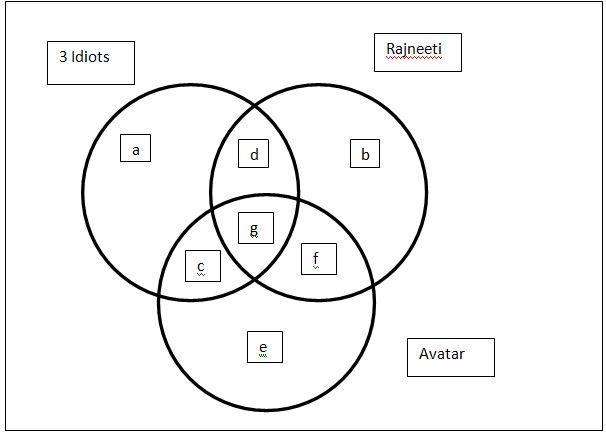
Now we know that
\[\{ (a + d + e + g) + (b + d + f + g) + (c + e + f + g)\} - (d + e + f) - 2g = a + b + c + d + e + f + g\]
\[61x + 46x + 29x - 25x - 2g = 97x\]
\[2g = 14x\]
\[g = 7x\]
Required value is \[7\% \]

Thus, Option (D) is correct.

Note: Here we must remember the algebra used in Venn diagram.
Some important properties of Sets are given below:
A. Idempotent Law is given as
(i) Union of two same sets \[A{\rm{ }} \cup {\rm{ }}A{\rm{ }} = {\rm{ }}A\]
(ii) Intersection of two same sets \[A{\rm{ }} \cap {\rm{ }}A{\rm{ }} = {\rm{ }}A\]

B. Associative Law is given as
(i) \[\left( {A{\rm{ }} \cup {\rm{ }}B} \right){\rm{ }} \cup {\rm{ }}C{\rm{ }} = {\rm{ }}A{\rm{ }} \cup {\rm{ }}\left( {B{\rm{ }} \cup {\rm{ }}C} \right)\]
(ii) \[\left( {A{\rm{ }} \cap {\rm{ }}B} \right){\rm{ }} \cap {\rm{ }}C{\rm{ }} = {\rm{ }}A{\rm{ }} \cap {\rm{ }}\left( {B{\rm{ }} \cap {\rm{ }}C} \right)\]

C. Commutative Law is given as
(i) \[A{\rm{ }} \cup {\rm{ }}B{\rm{ }} = {\rm{ }}B{\rm{ }} \cup {\rm{ }}A\]
(ii) \[A{\rm{ }} \cap {\rm{ }}B{\rm{ }} = {\rm{ }}B{\rm{ }} \cap {\rm{ }}A\]

D. Distributive law is given as
(i) \[A{\rm{ }} \cup {\rm{ }}\left( {B{\rm{ }} \cap {\rm{ }}C} \right){\rm{ }} = {\rm{ }}\left( {A{\rm{ }} \cup {\rm{ }}B} \right){\rm{ }} \cap {\rm{ }}\left( {A{\rm{ }} \cup {\rm{ }}C} \right)\]
(ii) \[A{\rm{ }} \cap {\rm{ }}\left( {B{\rm{ }} \cup {\rm{ }}C} \right){\rm{ }} = \left( {A{\rm{ }} \cap {\rm{ }}B} \right){\rm{ }} \cup {\rm{ }}\left( {A{\rm{ }} \cap {\rm{ }}C} \right)\]
Where A, B, C are set or subset of any universal set

E. De Morgan’s law is given as
(i) \[{\left( {A{\rm{ }} \cup B} \right)^c} = {A^c} \cap {\rm{ }}{B^c}\]
(ii) \[{\left( {A{\rm{ }} \cap B} \right)^c} = {A^c} \cup {\rm{ }}{B^c}\]
Where, \[{A^c},{B^c}\] is complement of set A and B respectively