




How Do You Calculate the Capacitance of a Spherical Capacitor?
A spherical capacitor consists of two concentric spherical shells separated by an insulating material, storing electrical energy through the separation of charges.
A spherical capacitor forms the basis for understanding how capacitance depends on geometry in three-dimensional symmetry, essential for advanced JEE Physics preparation.
Introduction to Spherical Capacitor
A spherical capacitor uses two hollow, concentric conducting spheres with radii $R_{1}$ and $R_{2}$, separated by air or a dielectric.
Unlike the parallel plate capacitor, a spherical capacitor's electric field is radially symmetric, which makes its study a cornerstone in Electrostatic Potential and Capacitance.
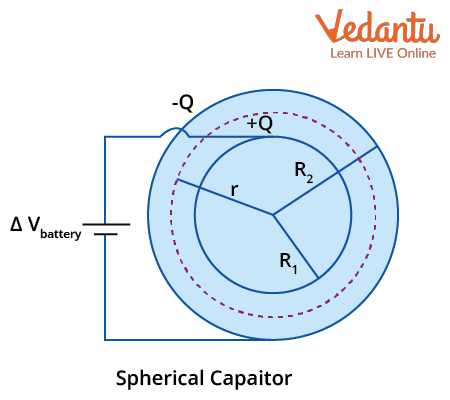
Visualizing a spherical capacitor is easy: imagine a small metallic sphere suspended inside a larger hollow metallic shell, with the gap filled by air or another insulator.
In practical terms, this geometry closely resembles the construction of certain high-voltage devices or the theoretical treatment of conducting spheres in space.
Working Principle and Key Features
When the inner and outer spheres carry equal and opposite charges $\pm Q$, a potential difference is established between the shells due to the electric field in the radial region.
The symmetry means the electric field exists only in the region between the shells and is given by $E = \dfrac{Q}{4 \pi \varepsilon_{0} r^{2}}$, derived using Gauss’s law.
Capacitance of Spherical Capacitor: Detailed Derivation
Applying Gauss’s law to a Gaussian surface of radius $r$ ($R_{1} < r < R_{2}$), the enclosed charge is $Q$ on the inner sphere, giving the electric field formula above.
The potential difference $V$ between the shells can be found by integrating the electric field:
$V = -\int_{R_{1}}^{R_{2}} E \, dr = \dfrac{Q}{4 \pi \varepsilon_{0}} \left(\dfrac{1}{R_{1}} - \dfrac{1}{R_{2}}\right)$
Substituting into the capacitance formula $C = \dfrac{Q}{V}$, we get:
$C = 4 \pi \varepsilon_{0} \dfrac{R_{1} R_{2}}{R_{2} - R_{1}}$
| Parameter | Spherical Capacitor Formula |
|---|---|
| Capacitance (Air) | $C = 4 \pi \varepsilon_{0} \dfrac{R_{1} R_{2}}{R_{2} - R_{1}}$ |
| Capacitance (Dielectric $\kappa$) | $C = 4 \pi \varepsilon_{0} \kappa \dfrac{R_{1} R_{2}}{R_{2} - R_{1}}$ |
The presence of a dielectric with constant $\kappa$ increases capacitance by a factor of $\kappa$, similar to other capacitor types.
A special case is when the outer shell is at infinity, yielding the capacitance of an isolated sphere: $C = 4 \pi \varepsilon_{0} R_{1}$.
Analogy and Visualization for JEE Aspirants
Visualize the energy storage like water held in the gap between two spherical bowls, where the potential builds up as charge accumulates.
Understanding this distribution helps connect the concept of potential difference to the physical arrangement of the shells in a Spherical Capacitance model.
Applications and Types of Spherical Capacitors
- Used in high-voltage capacitors for electric field symmetry
- Model for isolated charged conductors
- Standard derivation in JEE Physics syllabi
Spherical capacitors also help students understand real-life measurements, bridging theory and modern electrical engineering practice.
Energy Stored and JEE Implications
Energy stored in a spherical capacitor equals $U = \dfrac{1}{2} C V^{2}$, useful for calculating energy transfer in circuits or electrostatic setups.
Careful tracking of energy concepts connects spherical capacitors to broader capacitor theory, especially for Understanding Capacitance and its mathematical implications.
Role in Combination of Capacitors and Circuit Analysis
Spherical capacitors are rarely used in circuits directly but analyzing their combinations builds analogy for series-parallel networks.
Models of spherical capacitors help clarify the superposition principle when extending to other configurations, relating to Combination of Capacitors and their cumulative effects.
Solved Numerical Example: Spherical Capacitor Capacitance
A spherical capacitor has inner radius $R_{1} = 3\, \mathrm{cm}$, outer radius $R_{2} = 6\, \mathrm{cm}$, and is filled with air ($\varepsilon_{0}$). Calculate its capacitance.
Solution: Use $C = 4 \pi \varepsilon_{0} \dfrac{R_{1} R_{2}}{R_{2} - R_{1}}$ where $R_{1} = 0.03\, \mathrm{m}$, $R_{2} = 0.06\, \mathrm{m}$, $\varepsilon_{0} = 8.85 \times 10^{-12}\,\mathrm{F/m}$.
Plug in values: $C = 4 \times 3.14 \times 8.85 \times 10^{-12} \times \dfrac{0.03 \times 0.06}{0.06-0.03}$
$C \approx 2.0 \times 10^{-12} \,\mathrm{F}$ or $2.0\,\mathrm{pF}$.
Common JEE-Level Mistakes and Concepts
- Confusing formula with that for isolated sphere
- Ignoring dielectric effect in $C$ calculation
- Using wrong limits in potential integration
- Neglecting unit conversion from cm to m
- Misinterpreting field outside the capacitor system
Always verify correct formula, units, and whether the question asks for spherical capacitor or single isolated sphere for What is a Capacitor? based problems.
Practice Problem: Spherical Capacitor with Dielectric
If the space between $R_{1} = 2\,\mathrm{cm}$ and $R_{2} = 5\,\mathrm{cm}$ shells is filled with a dielectric of constant $\kappa = 4$, find $C$.
JEE Relevance and Conceptual Depth
Spherical capacitor questions probe your grasp of field symmetry and integration in 3D, which helps in Equivalent Capacitance Explained and advanced problem solving.
Thorough understanding aids not only in the Capacitors chapter but also builds skills for more challenging electromagnetism topics going forward.
Text-Based Related Topics for Further Study
- Derivation of capacitance for cylindrical capacitors
- Potential and field for charged spheres
- Dielectrics and their influence on capacitance
- Capacitor charging and discharging circuits
- Capacitance in series and parallel
- Gauss’s law applications in 3D conductors
- Energy density in electric fields
FAQs on What Is a Spherical Capacitor? Understanding Its Formula and Uses
1. What is a spherical capacitor?
A spherical capacitor is a device consisting of two concentric spherical conducting shells separated by an insulating material and used to store electric charge and energy.
Key features include:
- It consists of an inner sphere of radius a and an outer sphere of radius b (b > a)
- The region between the shells can be vacuum or filled with a dielectric
- It stores charge on the two spheres, one positive and one negative
2. Derive the formula for the capacitance of a spherical capacitor.
The capacitance C of a spherical capacitor depends on the radii of its shells and the permittivity of the medium between them.
The formula is:
- C = 4πε₀ε_r [(ab)/(b-a)], where:
- ε₀ = Permittivity of free space
- ε_r = Relative permittivity (dielectric constant) if dielectric is used
- a = Radius of the inner sphere
- b = Radius of the outer sphere
3. What are the applications of spherical capacitors?
Spherical capacitors are used where symmetrical electric fields are needed and high voltage insulation is important.
Applications include:
- Measuring instruments like electrometers
- High-voltage laboratories
- Demonstrating electrostatic principles in educational setups
- Precision charge storage in scientific experiments
4. How does inserting a dielectric change the capacitance of a spherical capacitor?
Inserting a dielectric increases the capacitance of a spherical capacitor by reducing the effective electric field strength between the shells.
Main effects:
- Capacitance formula becomes C = 4πε₀ε_r [(ab)/(b-a)]
- ε_r (the dielectric constant) > 1, so capacitance increases proportionally
- Enables higher charge storage at the same voltage
5. What is the electric field between the shells of a spherical capacitor?
The electric field (E) between the shells of a spherical capacitor varies with distance from the center.
In the region a < r < b (between the shells):
- E = (1 / (4πε₀)) × (Q / r²), directed radially outward (if inner shell is positive)
- No electric field outside the outer shell and inside the inner shell, as per Gauss's law
- Field is maximum just outside the inner shell
6. Why can't a single isolated sphere be called a capacitor?
An isolated sphere is not a true capacitor since a capacitor must have two conductors with equal and opposite charges separated by an insulator.
Key differences:
- A single sphere has only one conductor; potential is defined with respect to infinity
- A true capacitor (like a spherical capacitor) has two shells to store positive and negative charge
- Capacitance is then between the two shells, not relative to infinity
7. What is the capacitance of a spherical capacitor if the outer shell is earthed?
If the outer shell is earthed (connected to zero potential), the capacitance between the inner and outer shells remains:
- C = 4πε₀ [(ab)/(b–a)]
8. Give one example each of a real-life use and a theoretical analysis where spherical capacitors are preferred.
Spherical capacitors are chosen for specific applications due to their unique geometry.
Examples:
- Real-life use: Calibration devices in voltage standards
- Theoretical analysis: Deriving boundary conditions in electrostatics for spherically symmetric fields
9. Explain why the capacitance increases if the radius of the outer sphere (b) increases, keeping the inner radius (a) fixed.
The capacitance increases with a larger outer shell radius because the denominator (b–a) increases more slowly than the numerator (ab) in the formula C = 4πε₀ [(ab)/(b–a)].
Key points:
- Larger separation increases the effective area for charge storage
- Potential difference between the shells decreases for the same charge, increasing capacitance
- This is a key design principle in variable capacitors
10. Can a spherical capacitor ever have infinite capacitance? If so, under what condition?
A spherical capacitor theoretically has infinite capacitance when the outer sphere radius (b) approaches infinity.
Explanation:
- When b → ∞, (b–a) ≈ b, but ab / (b–a) → a
- In this case, the formula simplifies to C = 4πε₀a, which is the capacitance of an isolated sphere relative to infinity
- In practice, such a scenario is not achievable, but it aids conceptual understanding
























