




How to Calculate Equivalent Capacitance in Series and Parallel Circuits
The concept of equivalent capacitance is fundamental in analyzing electric circuits containing multiple capacitors. It allows complex capacitor arrangements to be replaced by a single capacitor with the same electrical effect between two points. This approach simplifies the calculation of total charge storage and voltage distribution in circuits using the rules of series and parallel combinations.
Definition of Equivalent Capacitance
Equivalent capacitance refers to the single capacitance that can replace a network of capacitors connected between two points, providing the same effect as the original combination. The calculation depends on the configuration of the capacitors in the circuit.
Capacitors in Parallel
When the terminals of multiple capacitors are connected such that both corresponding plates of all capacitors are connected together, the arrangement is known as a parallel combination. In this configuration, the potential difference across each capacitor is the same, while the total charge stored is the sum of the charges on each capacitor.
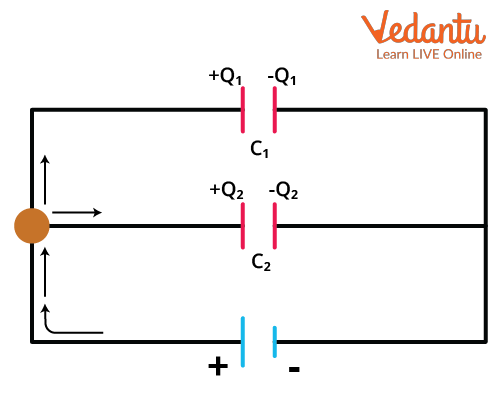
For $n$ capacitors, $C_1, C_2, C_3, \ldots, C_n$, connected in parallel, the equivalent capacitance $C_{eq}$ is given by the formula:
$C_{eq} = C_1 + C_2 + C_3 + \cdots + C_n$
This formula indicates a direct sum of capacitances, resulting in higher total capacitance with more capacitors in parallel.
Capacitors in Series
When capacitors are connected in series, the arrangement forms a chain where the end of one capacitor links to the beginning of the next. In this arrangement, the charge on each capacitor remains the same, but the voltage across the network is the sum of potential differences across individual capacitors.
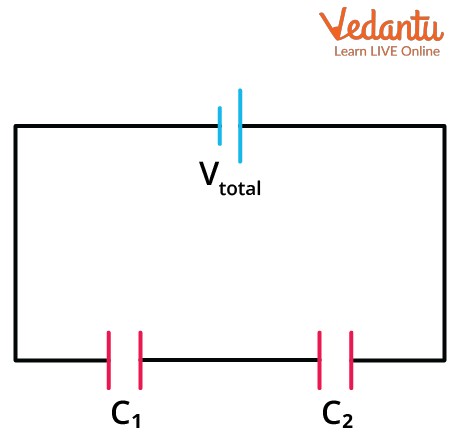
For $n$ capacitors in series, the expression for equivalent capacitance $C_{eq}$ is:
$\dfrac{1}{C_{eq}} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{C_3} + \cdots + \dfrac{1}{C_n}$
The value of $C_{eq}$ is always less than any individual capacitance in the series combination. More information on such combinations is provided at Combination of Capacitors.
Equivalent Capacitance in Complex Networks
In circuits containing both series and parallel combinations, reduce the network stepwise by replacing series or parallel groups with their equivalent capacitance until a single equivalent remains. This systematic method provides the total capacitance between two points and is used to analyze practical circuits.
Key Differences: Series vs. Parallel
| Series Combination | Parallel Combination |
|---|---|
| Same charge on each capacitor | Same voltage across each capacitor |
| Total voltage is sum of voltages | Total charge is sum of charges |
| $\dfrac{1}{C_{eq}}$ formula used | $C_{eq}$ is direct sum |
| $C_{eq}$ is less than any individual $C$ | $C_{eq}$ is greater than any individual $C$ |
Solved Example: Calculating Equivalent Capacitance
Consider three capacitors of $10~\mu\text{F}$, $3~\mu\text{F}$, and $8~\mu\text{F}$ connected in parallel across a potential difference. The equivalent capacitance is calculated as:
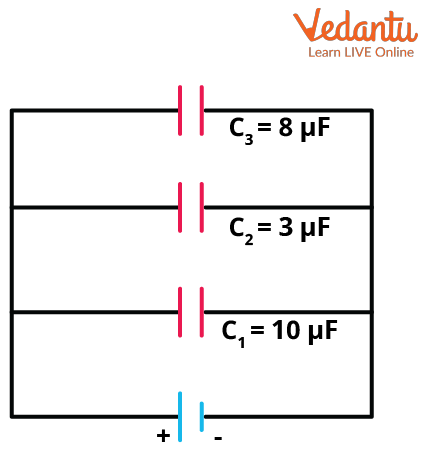
$C_{eq} = 10 + 3 + 8 = 21~\mu\text{F}$
If a potential difference of $5~\text{V}$ is applied, the total charge stored is $Q = C_{eq} \times V = 21 \times 10^{-6} \times 5 = 0.105~\text{mC}$.
Example: Series Capacitor Combination
For three capacitors in series with values $10~\mu\text{F}$, $3~\mu\text{F}$, and $8~\mu\text{F}$, the equivalent capacitance is:
$\dfrac{1}{C_{eq}} = \dfrac{1}{10} + \dfrac{1}{3} + \dfrac{1}{8}$
Calculate the sum: $0.1 + 0.333 + 0.125 = 0.558$. Thus, $C_{eq} \approx \dfrac{1}{0.558} \approx 1.8~\mu\text{F}$.
General Rules and Applications
- Parallel combination increases total capacitance
- Series combination decreases total capacitance
- Same charge flows through series combination
- Same voltage across parallel combination
- Always simplify stepwise for complex circuits
- Use equivalent capacitance to find total energy stored
Related Concepts in Capacitance
The calculation of equivalent capacitance is crucial in analyzing the behavior of RC circuits, determining energy storage, and understanding the grouping of capacitors in electronic designs. Further reading is available on Equivalent Capacitance and its connections with dielectric materials, which influence the total capacitance of a network as discussed at Capacitance and Dielectric.
Summary of Key Formulas
| Combination | Formula |
|---|---|
| Parallel | $C_{eq}=C_1+C_2+\cdots$ |
| Series | $\dfrac{1}{C_{eq}}=\dfrac{1}{C_1}+\dfrac{1}{C_2}+\cdots$ |
Understanding the rules of equivalent capacitance enables precise calculation of charge, voltage, and energy in electrical networks. For more structured problem-solving techniques, refer to RC Circuit and related problem sets.
FAQs on Understanding Equivalent Capacitance in Circuits
1. What is equivalent capacitance?
Equivalent capacitance is the single value of capacitance that can replace a combination of capacitors without changing the effect on the circuit.
- It simplifies complex capacitor networks.
- Used in series and parallel configurations for easier calculations.
- Helps in analyzing capacitor circuits as per CBSE syllabus.
2. How do you calculate the equivalent capacitance of capacitors in series?
To find the equivalent capacitance of capacitors in series, use the reciprocal sum formula:
- 1/C_eq = 1/C₁ + 1/C₂ + 1/C₃ + ...
- The total (C_eq) is always less than any individual capacitance.
- This is because the charge stored is the same, but voltage divides across each capacitor.
3. How do you calculate equivalent capacitance for capacitors connected in parallel?
For capacitors in parallel, the equivalent capacitance is the sum of all individual capacitors:
- C_eq = C₁ + C₂ + C₃ + ...
- The total increases since each capacitor stores charge at the same voltage.
- This method simplifies calculations in parallel circuits, per the CBSE chapter on capacitance.
4. What is the formula for equivalent capacitance in a combination of series and parallel connections?
For circuits with both series and parallel capacitors, calculate equivalent capacitance by:
- First, identify and simplify either the series or parallel groups.
- Apply the series formula (reciprocal sum) for series sections.
- Apply the parallel formula (direct sum) for parallel sections.
- Repeat until you find a single equivalent capacitance for the whole network.
5. What happens to the equivalent capacitance if more capacitors are added in parallel?
Adding capacitors in parallel increases the equivalent capacitance:
- This is because their individual capacitances add up.
- The circuit stores more total charge at the same voltage.
- It is helpful in applications requiring large capacitance, as per exam-focused topics.
6. What will be the effect on equivalent capacitance if a dielectric is inserted between the plates?
Inserting a dielectric increases the equivalent capacitance of a capacitor:
- This happens because the dielectric reduces the electric field, allowing more charge to be stored at the same voltage.
- The new capacitance becomes C' = kC, where k is the dielectric constant.
- Frequently appears in CBSE and board exams as conceptual questions.
7. Why is the equivalent capacitance of capacitors in series always less than any individual capacitance?
In a series connection, equivalent capacitance is always less than the smallest individual capacitor because:
- The total voltage divides, but all capacitors carry the same charge.
- It makes the combined effect weaker, lowering the net capacitance.
- This concept is important for understanding series circuits.
8. What is the SI unit of equivalent capacitance?
Equivalent capacitance is measured in the same SI unit as regular capacitance: Farad (F).
- Common subunits include microfarad (μF) and picofarad (pF).
- Always denote units while solving CBSE exam questions.
9. Can you explain the importance of equivalent capacitance in electrical circuits?
Equivalent capacitance helps analyze, design, and troubleshoot electrical circuits efficiently:
- Simplifies calculations for complex capacitor networks.
- Essential for understanding circuit behavior in physics, electronics, and engineering according to syllabus requirements.
- Reduces calculation errors and saves time in exams.
10. How can capacitors be arranged to achieve the maximum equivalent capacitance?
To achieve the maximum equivalent capacitance, connect all capacitors in parallel:
- This way, all individual values add up directly.
- Parallel arrangement is useful in applications needing large storage of charge.
- This is an important exam concept following CBSE Physics class 12.
11. What are the applications of equivalent capacitance in daily life?
Equivalent capacitance is widely used in real-life applications:
- Designing circuits in smartphones, TVs, and computers.
- Energy storage in power supplies and solar panels.
- Signal filtering and timing in electronic devices.
- Relevant for exams and practical projects.


































