




How Does Torque Work in Everyday Life?
Torque is an essential concept in rotational mechanics and plays a significant role in understanding how forces cause objects to rotate about an axis. Learning about torque builds a strong foundation for JEE Physics and is crucial for solving many mechanical problems.
What is Torque?
Torque refers to the tendency of a force to rotate an object about a specific axis or pivot point. It is a vector quantity, having both magnitude and direction, and is commonly represented by the Greek letter tau (τ). The magnitude of torque depends on both the magnitude of the applied force and the distance between the force's line of action and the axis of rotation.
The torque produced by a force can cause angular acceleration in a body, much like how linear forces cause changes in linear velocity. The effectiveness of torque increases when the force is applied farther from the rotational axis.
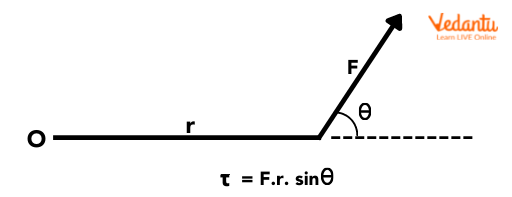
Torque Formula and Equations
Mathematically, torque is calculated as the cross product of the position vector (r) and the force vector (F). The standard torque equation is:
τ = r × F = rF sinθ
Here, τ is the torque, r is the distance from the axis to the point where force is applied, F is the magnitude of the force, and θ is the angle between r and F. The S.I. unit for torque is Newton-meter (N·m). This torque formula can be easily applied to many real-world and exam scenarios.
The torque expression highlights the dependence of rotational effectiveness on both strength and position of the applied force.
Direction of Torque: Right-Hand Thumb Rule
Since torque is a vector, its direction is determined by the right-hand thumb rule. If the fingers curl in the direction of rotation caused by the force, the extended thumb points in the direction of the torque vector. This helps identify if the rotation is clockwise or counterclockwise about the axis.
The direction of torque using right-hand thumb rule is crucial in vector analysis problems and ensures you apply the torque equation with correct sign conventions during your JEE exam.

Types of Torque
Depending on the effect it produces, torque is classified into different types. Understanding these types can help when analyzing various practical and exam problems involving rotation.
- Static torque: Does not cause angular acceleration
- Dynamic torque: Causes angular acceleration
Static torque examples include holding a door stationary against a force, while dynamic torque occurs when a force actually rotates the object, such as in engines or motors.
Everyday Applications of Torque
Torque finds its way into many everyday tools and devices that operate on rotational mechanics. Familiar examples are the torque wrench for fastening bolts, the torque screwdriver for precision work, and the torque multiplier used in heavy machinery. Concepts like the torque converter in vehicles allow engines to transmit and adapt rotational force efficiently.
Mechanisms in cars, machines, and household gadgets all depend on an optimal transfer of torque. Understanding applications will also help connect the theoretical torque formula with practical scenarios encountered in engineering and JEE Physics.
Key Factors Affecting Torque
Several variables influence how much torque is generated by a force:
- Magnitude of the applied force
- Distance from axis (lever arm length)
- Angle between force and lever arm
- Shape and size of rotating object
- Pivot or axis location relative to force
Tweaking these factors allows machines to maximize or control rotational effects, which is why devices such as the torque screwdriver or torque multiplier are designed for specific technical applications.
Physical Significance: Why Torque Matters
When dealing with rotational motion, torque determines how much an object will resist changes in its rotational state. This is closely related to a concept called the moment of inertia. For example, higher torque is required to accelerate heavier or larger objects about an axis, which is why engines must generate adequate torque output for cars to accelerate efficiently.
In rotational equilibrium, the sum of all torques acting on a system must be zero. This principle is widely applied to problems in mechanics, as well as practical tasks like balancing levers or designing machinery. Explore topics like Torque and Rotational Motion for deeper insight.
Relation to Moment of Inertia
The response of an object to applied torque depends on its moment of inertia. The moment of inertia quantifies the distribution of mass about an axis and determines how difficult it is to change an object's rotation. You can find detailed discussions and formulas in articles about Understanding Moment of Inertia or Moment of Inertia of Disc.
Torque in Modern Technology
Advancements in engineering have introduced equipment like the torque cast, a manufacturing method for automotive wheels. Additionally, torque ball assemblies are used for precise angular control, and reviews of their performance appear in technical literature and engineering forums. In the film industry, the term has even inspired the title of the “Torque movie” focused on motorcycle racing—a testament to its cultural significance!
Engineers and designers rely on calculations using the torque equation to ensure safety and efficiency in mechanical systems. Vedantu often emphasizes how mastering these concepts leads to better marks in JEE exams and builds practical knowledge for engineering careers.
Sample Table: Units and Comparison
It is helpful to summarize the key units and quantities associated with torque in a simple comparison table for quick revision:
| Quantity | Unit (S.I.) |
|---|---|
| Torque | Newton-meter (N·m) |
| Force | Newton (N) |
| Moment of Inertia | kg·m² |
Torque in Rotational Equilibrium
For a system to remain in rotational equilibrium, the sum of all torques acting about the axis must be zero. This principle applies when analyzing balanced beams, levers, and bridges. Engineers use this guideline to design stable structures.
You can find real scenarios calculated using the torque ball and get feedback from torque ball reviews regarding mechanical balance and performance.
Summary Points to Remember
Grasping the essentials of torque can transform your understanding of rotation in daily life and in exam problems. Key takeaways include:
- Torque is the rotational equivalent of force
- Calculated as τ = rF sinθ
- Directed using right-hand thumb rule
- Determines angular acceleration
- Influenced by lever arm length and force magnitude
- Found in tools like torque wrench and torque screwdriver
Strengthen your foundational skills by exploring related topics such as Torque on Electric Dipole and ensuring you practice problems from Vedantu study resources. Mastery of torque will support your success in JEE and future engineering applications.
FAQs on What Is Torque in Physics?
1. What is torque in physics?
Torque is the turning effect of a force applied to a rotational object about an axis.
- It is also called the moment of force.
- Torque determines how effectively a force can rotate an object.
- The SI unit of torque is Newton-metre (N·m).
- Mathematically, Torque (τ) = Force (F) × Perpendicular distance (r) from the axis of rotation.
2. What is the formula for torque?
The formula for torque expresses how force causes rotation about an axis.
- Torque (τ) = Force (F) × Perpendicular distance (r).
- If the force is not perpendicular:
τ = F × r × sinθ
- Here, θ is the angle between force and the position vector.
- Unit: Newton-metre (N·m).
3. What is the SI unit of torque?
Torque is measured in the SI unit of Newton-metre (N·m).
- 1 Newton-metre means a force of 1 Newton acting at a perpendicular distance of 1 metre from the axis of rotation.
- It is symbolised as N·m.
4. What are some examples of torque in daily life?
Torque can be observed whenever a rotational motion is produced by applying force at a distance from a pivot.
Some common examples include:
- Turning a door knob or tightening a screw with a screwdriver
- Opening a door by pushing at its edge
- Using a spanner to loosen a nut
- Riding a bicycle and pedalling
- Steering a car wheel
5. How is torque different from force?
Torque and force are related but represent different physical quantities.
- Force is a push or pull that can move an object in a straight line.
- Torque is the rotational effect of a force applied at a distance from an axis.
- Force causes linear motion, while torque causes rotational motion.
6. What factors affect the magnitude of torque?
The magnitude of torque depends on:
- Magnitude of force (F): Greater force increases torque.
- Perpendicular distance (r) from the axis: Larger distance increases torque.
- Angle (θ): Maximum torque occurs when force is applied perpendicular (sin90° = 1) to the lever arm.
7. What is the direction of torque?
The direction of torque is determined using the right-hand rule.
- Curl the fingers of your right hand in the direction of rotation caused by the force.
- Your thumb points in the direction of the torque vector.
- Conventionally, anticlockwise torque is positive and clockwise torque is negative.
8. What is the principle of moments?
The principle of moments states that for an object in rotational equilibrium, the sum of the clockwise moments about a point equals the sum of anticlockwise moments about the same point.
- Mathematically: Σ clockwise moments = Σ anticlockwise moments.
- This principle is used to solve for unknown forces or distances in levers and beams.
9. What is the relation between torque and angular acceleration?
Torque is directly proportional to the angular acceleration of a rotating body.
- Given by the equation: τ = I × α.
- τ: Torque
- I: Moment of inertia
- α: Angular acceleration
10. How does torque relate to rotational equilibrium?
Rotational equilibrium occurs when the total torque acting on an object is zero.
- The object will not rotate if Στ = 0.
- Sum of clockwise torque equals sum of anticlockwise torque.
- Used in balancing beams and seesaws.
























