
Let $f:R \to R$ be a function defined by $f(x) = \left\{ k - 2x,{\text{ if }}x \leqslant - 1 \\
2x + 3,{\text{ if }}x > - 1 \\
\right.$ , of $f$has a local minimum at $x = - 1$, then possible values of $k$is.
A. $1$
B. $0$
C. $ - \dfrac{1}{2}$
D. $ - 1$
Answer
216k+ views
Hint: Here, we have to find out the possible values of $k$. In this question we, have to take limits to find out the value of $k$. Firstly, we take the function $f(x) > - 1$ and take the limit of this function and find out the $f(x)$.
Secondly, we take the function $f(x) \leqslant - 1$and take a limit of the function and calculate the value of $f(x)$in terms of $k$.We are given the local minimum at $x = - 1$.Now these three conditions and find the value of .
Complete step by step solution:
We have;
$f(x) = \left\{
k - 2x,{\text{ if }}x \leqslant - 1 \\
2x + 3,{\text{ if }}x > - 1 \\
\right.$
Let us take the limit of a function $f(x) > - 1$ we get;
$
\mathop {\lim }\limits_{x \to - {1^ + }} f(x) = \mathop {\lim }\limits_{x \to - {1^ + }} (2x + 3) \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} f(x) = 2( - 1) + 3 \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} f(x) = - 2 + 3 \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} f(x) = + 1 \\
$
Similarly, take the function with limit $f(x) \leqslant - 1$ we have,
$
\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \mathop {\lim }\limits_{x \to - {1^ - }} (k - 2x) \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ - }} f(x) = k - 2( - 1) \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ - }} f(x) = k + 2 \\
$
Here we are having the local minimum of function $f(x)$at $x = - 1$.
Therefore, we can write the function as follows:
$f( - {1^ + }) \geqslant f( - 1) \geqslant f( - {1^ - })$
Putting all the values we get;
$1 \geqslant k + 2$
Subtract from both sides we get;
$
1 - 2 \geqslant k + 2 - 2 \\
\Rightarrow - 1 \geqslant k \\
\Rightarrow k \leqslant - 1 \\
$
Therefore, according to the local minimum of the function, we can take the possible value of $k$ is taken as$ - 1$.
Option ‘D’ is correct
Note: In this type of question, we must consider the conditions for each function we have given, and we must determine the limit of the given variable based on the conditions. Always keep an eye out for signs of inequity in the questions, such as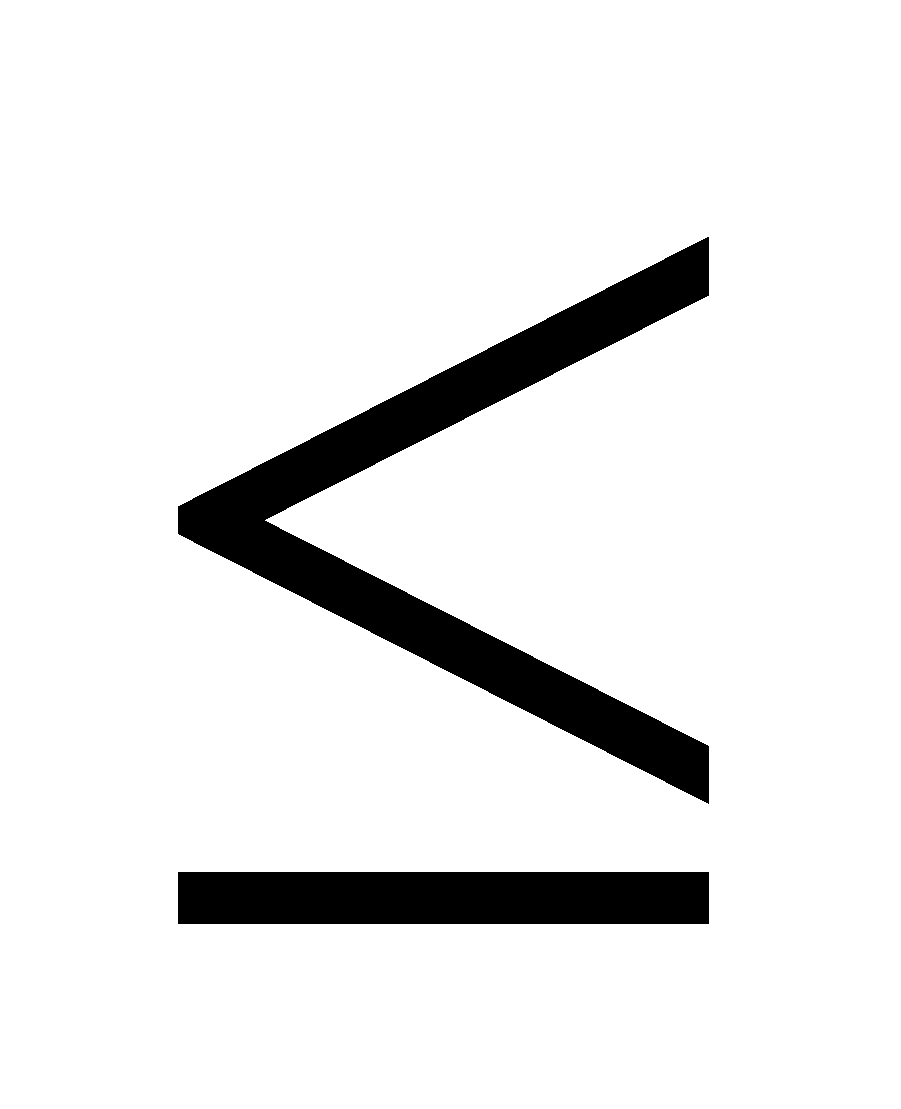 (less than equal to),
(less than equal to),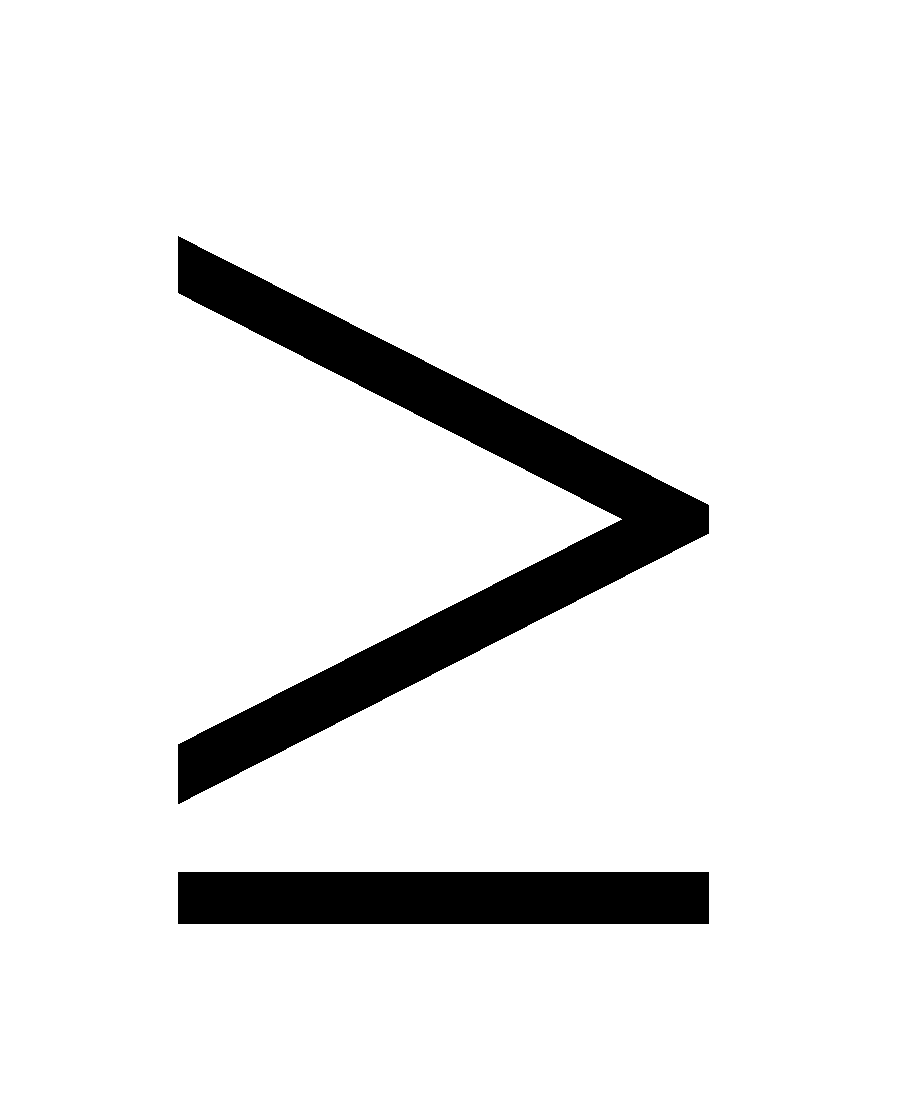 (greater than equal to),
(greater than equal to), (less than),
(less than),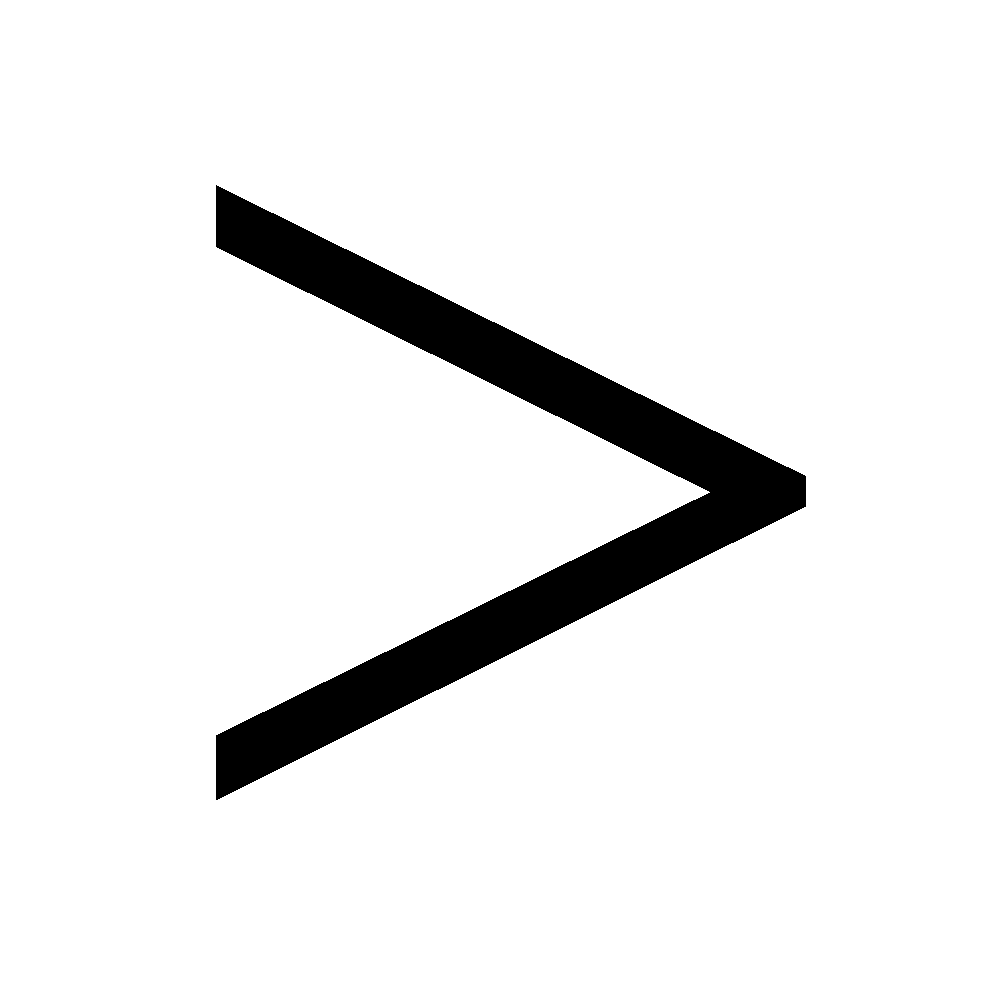 and (greater than). If we took 'x' conditions in a function. Always solve inequalities by adding, subtracting, multiplying, or dividing both sides until the variable is left alone. Do not attempt to solve it directly.
and (greater than). If we took 'x' conditions in a function. Always solve inequalities by adding, subtracting, multiplying, or dividing both sides until the variable is left alone. Do not attempt to solve it directly.
Secondly, we take the function $f(x) \leqslant - 1$and take a limit of the function and calculate the value of $f(x)$in terms of $k$.We are given the local minimum at $x = - 1$.Now these three conditions and find the value of .
Complete step by step solution:
We have;
$f(x) = \left\{
k - 2x,{\text{ if }}x \leqslant - 1 \\
2x + 3,{\text{ if }}x > - 1 \\
\right.$
Let us take the limit of a function $f(x) > - 1$ we get;
$
\mathop {\lim }\limits_{x \to - {1^ + }} f(x) = \mathop {\lim }\limits_{x \to - {1^ + }} (2x + 3) \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} f(x) = 2( - 1) + 3 \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} f(x) = - 2 + 3 \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} f(x) = + 1 \\
$
Similarly, take the function with limit $f(x) \leqslant - 1$ we have,
$
\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \mathop {\lim }\limits_{x \to - {1^ - }} (k - 2x) \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ - }} f(x) = k - 2( - 1) \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ - }} f(x) = k + 2 \\
$
Here we are having the local minimum of function $f(x)$at $x = - 1$.
Therefore, we can write the function as follows:
$f( - {1^ + }) \geqslant f( - 1) \geqslant f( - {1^ - })$
Putting all the values we get;
$1 \geqslant k + 2$
Subtract from both sides we get;
$
1 - 2 \geqslant k + 2 - 2 \\
\Rightarrow - 1 \geqslant k \\
\Rightarrow k \leqslant - 1 \\
$
Therefore, according to the local minimum of the function, we can take the possible value of $k$ is taken as$ - 1$.
Option ‘D’ is correct
Note: In this type of question, we must consider the conditions for each function we have given, and we must determine the limit of the given variable based on the conditions. Always keep an eye out for signs of inequity in the questions, such as
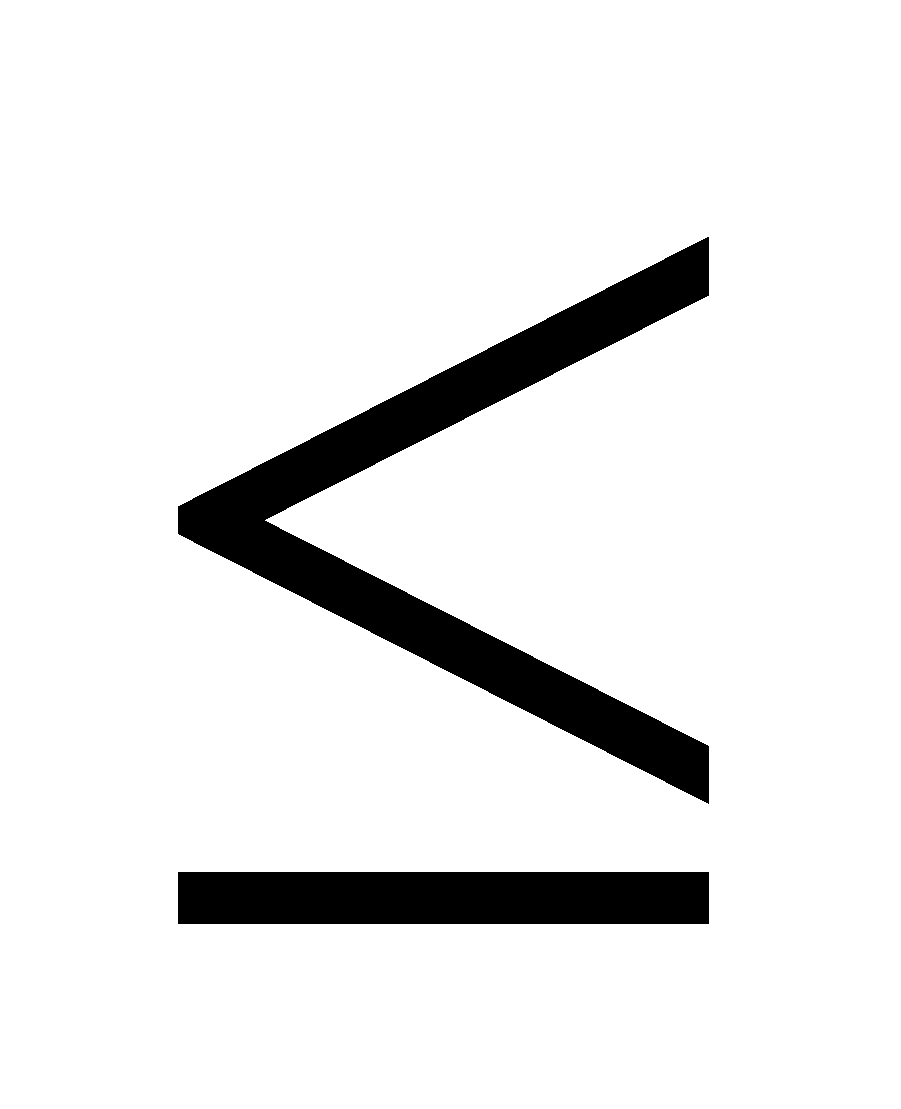 (less than equal to),
(less than equal to), (greater than equal to),
(greater than equal to), (less than),
(less than), and (greater than). If we took 'x' conditions in a function. Always solve inequalities by adding, subtracting, multiplying, or dividing both sides until the variable is left alone. Do not attempt to solve it directly.
and (greater than). If we took 'x' conditions in a function. Always solve inequalities by adding, subtracting, multiplying, or dividing both sides until the variable is left alone. Do not attempt to solve it directly.Recently Updated Pages
JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance

Understanding the Electric Field of a Uniformly Charged Ring

Understanding Average and RMS Value in Electrical Circuits




