
In the given mesh, each resistor has resistance R. The effective resistance between the terminals A and B is
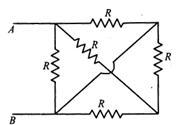
A. \[\dfrac{{3R}}{8}\]
B. \[\dfrac{R}{2}\]
C. \[R\]
D. \[2R\]
Answer
216k+ views
Hint: The equivalent resistance is the sum of the aggregate resistances connected in parallel or series. The circuit is essentially built in either series or parallel. We must use the equivalent resistance formula to calculate the equivalent resistance between terminals A and B.
Formula used:
To solve this topic, we must first understand that parallel resistance connection is given by\[\dfrac{1}{{Rp}} = \dfrac{1}{{R1}} + \dfrac{1}{{R2}} + \dfrac{1}{{R3}}....... + \dfrac{1}{{RN}}\].
Complete answer:
We have been provided in the question that,
Each resistor has resistance R
We are provided with the circuit diagram below,
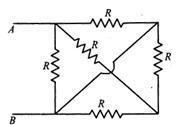
On simplifying the above mesh into an effective circuit, we get
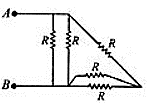
Then, evaluating the resistance from the end of the circuit to the terminals as follows:
Since the two resistors at the end (bottom) are parallel, we get their equivalent resistance as
$\begin{align}
& \frac{1}{{{R}_{e1}}}=\frac{1}{R}+\frac{1}{R} \\
& \Rightarrow \frac{1}{{{R}_{e1}}}=\frac{2}{R} \\
& \Rightarrow {{R}_{e1}}=\frac{R}{2} \\
\end{align}$
Then the circuit becomes
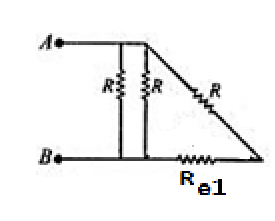
So, the last two resistors come together in series. So, we get their equivalent resistance as
\[\begin{align}
& {{R}_{e2}}=R+{{R}_{e1}} \\
& \Rightarrow {{R}_{e2}}=R+\frac{R}{2} \\
& \Rightarrow {{R}_{e2}}=\frac{3R}{2} \\
\end{align}\]
Now, the circuit becomes

So, the remaining three resistors exist in parallel connection. Thus, their equivalent resistance is given by ${{R}_{AB}}$ and it is calculated as
$\begin{align}
& \frac{1}{{{R}_{AB}}}=\frac{1}{R}+\frac{1}{R}+\frac{1}{{{R}_{e2}}} \\
& \Rightarrow \frac{1}{{{R}_{AB}}}=\frac{2}{R}+\frac{1}{\left( \frac{3R}{2} \right)} \\
& \Rightarrow \frac{1}{{{R}_{AB}}}=\frac{2}{R}+\frac{2}{3R}=\frac{8}{3R} \\
& \therefore {{R}_{AB}}=\frac{3R}{8} \\
\end{align}$
Therefore, the effective resistance between the terminals A and B is \[\frac{{3R}}{8}\].
Hence, option A is the correct answer
Note: We should expect a parallel circuit to have more than two channels for current to flow through it. The total current coming from the source will be equal to the sum of the currents going via each of the pathways. In a series circuit, however, the overall resistance equals the sum of the individual resistances. Similarly, the voltage supplied in the series circuit will equal the sum of all the individual voltage decreases.
Formula used:
To solve this topic, we must first understand that parallel resistance connection is given by\[\dfrac{1}{{Rp}} = \dfrac{1}{{R1}} + \dfrac{1}{{R2}} + \dfrac{1}{{R3}}....... + \dfrac{1}{{RN}}\].
Complete answer:
We have been provided in the question that,
Each resistor has resistance R
We are provided with the circuit diagram below,

On simplifying the above mesh into an effective circuit, we get

Then, evaluating the resistance from the end of the circuit to the terminals as follows:
Since the two resistors at the end (bottom) are parallel, we get their equivalent resistance as
$\begin{align}
& \frac{1}{{{R}_{e1}}}=\frac{1}{R}+\frac{1}{R} \\
& \Rightarrow \frac{1}{{{R}_{e1}}}=\frac{2}{R} \\
& \Rightarrow {{R}_{e1}}=\frac{R}{2} \\
\end{align}$
Then the circuit becomes

So, the last two resistors come together in series. So, we get their equivalent resistance as
\[\begin{align}
& {{R}_{e2}}=R+{{R}_{e1}} \\
& \Rightarrow {{R}_{e2}}=R+\frac{R}{2} \\
& \Rightarrow {{R}_{e2}}=\frac{3R}{2} \\
\end{align}\]
Now, the circuit becomes

So, the remaining three resistors exist in parallel connection. Thus, their equivalent resistance is given by ${{R}_{AB}}$ and it is calculated as
$\begin{align}
& \frac{1}{{{R}_{AB}}}=\frac{1}{R}+\frac{1}{R}+\frac{1}{{{R}_{e2}}} \\
& \Rightarrow \frac{1}{{{R}_{AB}}}=\frac{2}{R}+\frac{1}{\left( \frac{3R}{2} \right)} \\
& \Rightarrow \frac{1}{{{R}_{AB}}}=\frac{2}{R}+\frac{2}{3R}=\frac{8}{3R} \\
& \therefore {{R}_{AB}}=\frac{3R}{8} \\
\end{align}$
Therefore, the effective resistance between the terminals A and B is \[\frac{{3R}}{8}\].
Hence, option A is the correct answer
Note: We should expect a parallel circuit to have more than two channels for current to flow through it. The total current coming from the source will be equal to the sum of the currents going via each of the pathways. In a series circuit, however, the overall resistance equals the sum of the individual resistances. Similarly, the voltage supplied in the series circuit will equal the sum of all the individual voltage decreases.
Recently Updated Pages
Wheatstone Bridge Explained: Working, Formula & Uses

Young’s Double Slit Experiment Derivation Explained

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance

Understanding the Electric Field of a Uniformly Charged Ring

Understanding Average and RMS Value in Electrical Circuits




