
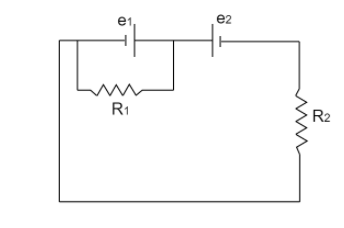
In the circuit shown, ${{e}_{1}}={{e}_{2}}=2V$ and their internal resistances are $0.5\Omega $ each. ${{R}_{1}}=0.5\Omega $ and ${{R}_{2}}=1.5\Omega $ . The current through ${{R}_{1}}$ is
Answer
218.7k+ views
Hint Kirchoff’s current law states that the current entering a circuit junction will be the same as the current exiting a circuit junction. It can also be defined as the sum of the currents at a junction in a circuit is always zero, taking into account the direction of the current flow. Apply this law and Ohm’s law for the circuit given and proceed.
Complete Step by step answer
Let us assume that the current flow from the first cell to be ${{I}_{1}}$ and the current flow from the second cell to be ${{I}_{2}}$ . The currents from both cells will enter the junction and pass through the resistor from Kirchoff’s current law. Therefore, we can say that the current through the resistor ${{R}_{1}}$ to be ${{I}_{1}}+{{I}_{2}}$ .
We can find the current through the first cell by using Ohm’s law.
${{e}_{2}}={{I}_{2}}({{R}_{2}}+{{r}_{2}})$
Here, ${{r}_{2}}$ denotes the internal resistance of the second cell.
By substituting the given values of internal resistance of the second cell, the resistance of the second resistor, and potential due to the second cell, we get
$2={{I}_{2}}(1.5+0.5)$
$\Rightarrow {{I}_{2}}=\frac{2}{2}$
$\Rightarrow {{I}_{2}}=1A$
Applying ohm’s law to the first resistor, we get
${{e}_{1}}={{I}_{1}}{{r}_{1}}+({{I}_{1}}+{{I}_{2}}){{R}_{1}}$
Here, ${{r}_{1}}$ denotes the internal resistance of the first cell.
By substituting the values of the potential of the first cell, the internal resistance of the first cell, the resistance of the first resistor, and by substituting the calculated value of the current ${{I}_{2}}$ , we get
$2=0.5{{I}_{1}}+({{I}_{1}}+1)1.5$
By simplification, we get
${{I}_{1}}=0.25A$
Therefore, the total current that passes through the first resistor ${{R}_{1}}$ is given by
${{I}_{1}}+{{I}_{2}}=1+0.25$
$\Rightarrow {{I}_{1}}+{{I}_{2}}=1.25A$
Hence, $1.25A$ is the total current that passes through the resistor ${{R}_{1}}$ .
Note
The internal resistance of a cell is different from the load in a circuit. Usually, the internal resistances are even neglected as they are very small when compared to the load resistance. Internal resistance can be caused by either corrosion or due to sulfation.
Complete Step by step answer
Let us assume that the current flow from the first cell to be ${{I}_{1}}$ and the current flow from the second cell to be ${{I}_{2}}$ . The currents from both cells will enter the junction and pass through the resistor from Kirchoff’s current law. Therefore, we can say that the current through the resistor ${{R}_{1}}$ to be ${{I}_{1}}+{{I}_{2}}$ .
We can find the current through the first cell by using Ohm’s law.
${{e}_{2}}={{I}_{2}}({{R}_{2}}+{{r}_{2}})$
Here, ${{r}_{2}}$ denotes the internal resistance of the second cell.
By substituting the given values of internal resistance of the second cell, the resistance of the second resistor, and potential due to the second cell, we get
$2={{I}_{2}}(1.5+0.5)$
$\Rightarrow {{I}_{2}}=\frac{2}{2}$
$\Rightarrow {{I}_{2}}=1A$
Applying ohm’s law to the first resistor, we get
${{e}_{1}}={{I}_{1}}{{r}_{1}}+({{I}_{1}}+{{I}_{2}}){{R}_{1}}$
Here, ${{r}_{1}}$ denotes the internal resistance of the first cell.
By substituting the values of the potential of the first cell, the internal resistance of the first cell, the resistance of the first resistor, and by substituting the calculated value of the current ${{I}_{2}}$ , we get
$2=0.5{{I}_{1}}+({{I}_{1}}+1)1.5$
By simplification, we get
${{I}_{1}}=0.25A$
Therefore, the total current that passes through the first resistor ${{R}_{1}}$ is given by
${{I}_{1}}+{{I}_{2}}=1+0.25$
$\Rightarrow {{I}_{1}}+{{I}_{2}}=1.25A$
Hence, $1.25A$ is the total current that passes through the resistor ${{R}_{1}}$ .
Note
The internal resistance of a cell is different from the load in a circuit. Usually, the internal resistances are even neglected as they are very small when compared to the load resistance. Internal resistance can be caused by either corrosion or due to sulfation.
Recently Updated Pages
A square frame of side 10 cm and a long straight wire class 12 physics JEE_Main

The work done in slowly moving an electron of charge class 12 physics JEE_Main

Two identical charged spheres suspended from a common class 12 physics JEE_Main

According to Bohrs theory the timeaveraged magnetic class 12 physics JEE_Main

ill in the blanks Pure tungsten has A Low resistivity class 12 physics JEE_Main

The value of the resistor RS needed in the DC voltage class 12 physics JEE_Main

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Centrifugal Force in Physics

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance




