Question

In a triangle, ABC right angled at C, the value of $\tan A+\tan B$ is [Pb. CET 1990; Karnataka CET 1999; MP PET 2001]
A. a+b
B. $\dfrac{{{a}^{2}}}{bc}$
C. $\dfrac{{{b}^{2}}}{ac}$
D. $\dfrac{{{c}^{2}}}{ab}$

Answer 1

Hint:
In the question, we have given a right-angled triangle. In order to obtain the value of $\tan A+\tan B$, we have to find the value for $\tan A$ and $\tan B$ using the trigonometric ratio of the tangent of an angle. Then add up the values. Use the Pythagoras theorem for a right-angled triangle and make a possible substitution. Now compare the obtained result with the given options.

Formula Used:
When it comes to the angle of $90$ degrees, we are aware that it is a right-angled triangle with a base, a perpendicular, and a hypotenuse then,
$\tan A = \dfrac{Perpendicular}{Base}$.

Complete step-by-step solution:
We have given a triangle $ABC$ with right-angles at $C$;

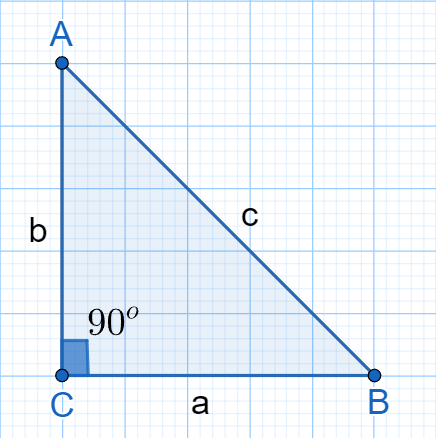
According to the Pythagoras theorem, we can write;
$c^2=a^2+b^2…(i)$
Therefore,
$\tan A=\dfrac{a}{b}\\
\tan B=\dfrac{b}{a}$
Now,
$\tan A+\tan B\\
=\dfrac{a}{b}+\dfrac{b}{a}\\
=\dfrac{a^2+b^2}{ab}$
Substitute eq (i)
$=\dfrac{c^2}{ab}$
Hence, $\tan A+\tan B=\dfrac{c^2}{ab}$

So, option D is correct.

Note:
Keep in mind that such type of question requires knowledge of the basic trigonometric ratios. The trigonometric ratios of a given acute angle are the ratios of the sides of a right-angled triangle concerning that angle. Therefore, the ratio of the angle's opposite and adjacent sides is referred to as the tan of the angle. Remember the base of the right triangle is located next to the opposite side, which is the perpendicular side. So carefully find the value of tan at $A$ and $B$.