
If \[y = mx\] be one of the bisectors of the angle between the lines \[a{x^2}\; - {\text{ }}2hxy{\text{ }} + {\text{ }}b{y^2}\; = {\text{ }}0\], then
A. \[h\left( {1 + {m^2}} \right) + m\left( {a - b} \right) = 0\]
B. \[h\left( {1 - {m^2}} \right) + m\left( {a + b} \right) = 0\]
C. \[h\left( {1 - {m^2}} \right) + m\left( {a - b} \right) = 0\]
D. \[h\left( {1 + {m^2}} \right) + m\left( {a + b} \right) = 0\]
Answer
219k+ views
Hint: In this question, we need to find the condition for which \[y = mx\] is one of the bisectors of the angle between the lines \[a{x^2}\; - {\text{ }}2hxy{\text{ }} + {\text{ }}b{y^2}\; = {\text{ }}0\]. For this, we have to use the following formulae and after simplification we will get the desired result.
Formula used: The equation of a straight line is \[y = mx + c\] and its slope is \[m = \tan \theta \] .
Here, \[\theta \] is the angle subtended by the angle bisector of the pair of straight lines with the positive x-axis direction.
Also, we will use some trigonometric identities here.
\[\tan \left( {A + B} \right) = \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}}\] and \[\tan 2\theta = \dfrac{{2\tan \theta }}{{1 - {{\tan }^2}\theta }}\]
Complete step-by-step answer:
Let us assume that the equations \[y - {m_1}x = 0\] and \[y - {m_2}x = 0\] are two straight lines denoted by the given equation of a pair of straight lines.
So, we can say that \[{m_1} = \tan \alpha \]and \[{m_2} = \tan \beta \] and also \[\beta > \alpha \]
Thus, we get
\[\left( {y - {m_1}x} \right)\left( {y - {m_2}x} \right) = {y^2} - \dfrac{{2h}}{b}xy + \dfrac{a}{b}{x^2}\]
\[\left( y \right)\left( {y - {m_2}x} \right) - {m_1}x\left( {y - {m_2}x} \right) = {y^2} - \dfrac{{2h}}{b}xy + \dfrac{a}{b}{x^2}\]
\[{y^2} - xy{m_2} - xy{m_1} + {m_1}{m_2}{x^2} = {y^2} - \dfrac{{2h}}{b}xy + \dfrac{a}{b}{x^2}\]
\[{y^2} - \left( {{m_1} + {m_2}} \right)xy + \left( {{m_1}{m_2}} \right){x^2} = {y^2} - \dfrac{{2h}}{b}xy + \dfrac{a}{b}{x^2}\]
By comparing coefficients of left and right side, we get
\[{m_1} + {m_2} = \dfrac{{2h}}{b}\] and \[{m_1}{m_2} = \dfrac{a}{b}\]
As \[\beta > \alpha \], we can say that \[\theta - \alpha = \beta - \theta \]
For better understanding, consider the following figure for this.
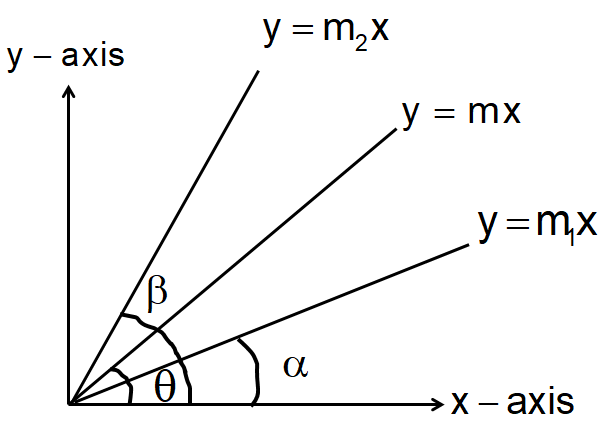
Image: Graphical representation of given information
That means, \[\theta + \theta = \beta + \alpha \]
That is \[\beta + \alpha = 2\theta \]
Now, by taking tan on both sides, we get
\[\tan \left( {\alpha + \beta } \right) = \tan \left( {2\theta } \right)\]
But \[\tan \left( {A + B} \right) = \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}}\] and \[\tan 2\theta = \dfrac{{2\tan \theta }}{{1 - {{\tan }^2}\theta }}\]
Thus, we get
\[\dfrac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} = \dfrac{{\tan \theta }}{{1 - {{\tan }^2}\theta }}\]
\[\dfrac{{{m_1} + {m_2}}}{{1 - {m_1} \times {m_2}}} = \dfrac{{2m}}{{1 - {m^2}}}\]
But \[{m_1} + {m_2} = \dfrac{{2h}}{b}\] and \[{m_1}{m_2} = \dfrac{a}{b}\]
So, we get
\[\dfrac{{\dfrac{{2h}}{b}}}{{1 - \dfrac{a}{b}}} = \dfrac{{2m}}{{1 - {m^2}}}\]
Let us simplify this.
\[\dfrac{{\dfrac{{2h}}{b}}}{{\dfrac{{b - a}}{b}}} = \dfrac{{2m}}{{1 - {m^2}}}\]
\[\dfrac{{2h}}{b} \times \dfrac{b}{{b - a}} = \dfrac{{2m}}{{1 - {m^2}}}\]
\[\dfrac{h}{{b - a}} = \dfrac{m}{{1 - {m^2}}}\]
By doing cross multiplication, we get
\[h\left( {1 - {m^2}} \right) = m\left( {b - a} \right)\]
\[h\left( {1 - {m^2}} \right) = - m\left( {a - b} \right)\]
That is \[h\left( {1 - {m^2}} \right) + m\left( {a - b} \right) = 0\]
Hence, If \[y = mx\] be one of the bisectors of the angle between the lines \[a{x^2}\; - {\text{ }}2hxy{\text{ }} + {\text{ }}b{y^2}\; = {\text{ }}0\], then \[h\left( {1 - {m^2}} \right) + m\left( {a - b} \right) = 0\]
Therefore, the correct option is (C).
Note: Here, generally students solve this example without a graphical representation of the given information but it makes it easy to solve this problem using a graphical representation. Also, it is to use tangent identity to get the desired result as the slope of a line is expressed in terms of a tangent trigonometric function.
Formula used: The equation of a straight line is \[y = mx + c\] and its slope is \[m = \tan \theta \] .
Here, \[\theta \] is the angle subtended by the angle bisector of the pair of straight lines with the positive x-axis direction.
Also, we will use some trigonometric identities here.
\[\tan \left( {A + B} \right) = \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}}\] and \[\tan 2\theta = \dfrac{{2\tan \theta }}{{1 - {{\tan }^2}\theta }}\]
Complete step-by-step answer:
Let us assume that the equations \[y - {m_1}x = 0\] and \[y - {m_2}x = 0\] are two straight lines denoted by the given equation of a pair of straight lines.
So, we can say that \[{m_1} = \tan \alpha \]and \[{m_2} = \tan \beta \] and also \[\beta > \alpha \]
Thus, we get
\[\left( {y - {m_1}x} \right)\left( {y - {m_2}x} \right) = {y^2} - \dfrac{{2h}}{b}xy + \dfrac{a}{b}{x^2}\]
\[\left( y \right)\left( {y - {m_2}x} \right) - {m_1}x\left( {y - {m_2}x} \right) = {y^2} - \dfrac{{2h}}{b}xy + \dfrac{a}{b}{x^2}\]
\[{y^2} - xy{m_2} - xy{m_1} + {m_1}{m_2}{x^2} = {y^2} - \dfrac{{2h}}{b}xy + \dfrac{a}{b}{x^2}\]
\[{y^2} - \left( {{m_1} + {m_2}} \right)xy + \left( {{m_1}{m_2}} \right){x^2} = {y^2} - \dfrac{{2h}}{b}xy + \dfrac{a}{b}{x^2}\]
By comparing coefficients of left and right side, we get
\[{m_1} + {m_2} = \dfrac{{2h}}{b}\] and \[{m_1}{m_2} = \dfrac{a}{b}\]
As \[\beta > \alpha \], we can say that \[\theta - \alpha = \beta - \theta \]
For better understanding, consider the following figure for this.
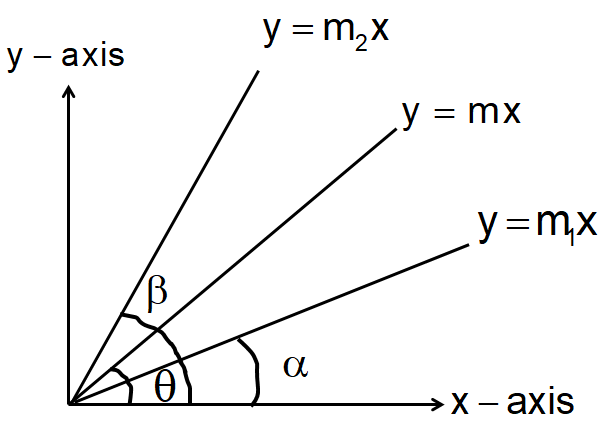
Image: Graphical representation of given information
That means, \[\theta + \theta = \beta + \alpha \]
That is \[\beta + \alpha = 2\theta \]
Now, by taking tan on both sides, we get
\[\tan \left( {\alpha + \beta } \right) = \tan \left( {2\theta } \right)\]
But \[\tan \left( {A + B} \right) = \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}}\] and \[\tan 2\theta = \dfrac{{2\tan \theta }}{{1 - {{\tan }^2}\theta }}\]
Thus, we get
\[\dfrac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} = \dfrac{{\tan \theta }}{{1 - {{\tan }^2}\theta }}\]
\[\dfrac{{{m_1} + {m_2}}}{{1 - {m_1} \times {m_2}}} = \dfrac{{2m}}{{1 - {m^2}}}\]
But \[{m_1} + {m_2} = \dfrac{{2h}}{b}\] and \[{m_1}{m_2} = \dfrac{a}{b}\]
So, we get
\[\dfrac{{\dfrac{{2h}}{b}}}{{1 - \dfrac{a}{b}}} = \dfrac{{2m}}{{1 - {m^2}}}\]
Let us simplify this.
\[\dfrac{{\dfrac{{2h}}{b}}}{{\dfrac{{b - a}}{b}}} = \dfrac{{2m}}{{1 - {m^2}}}\]
\[\dfrac{{2h}}{b} \times \dfrac{b}{{b - a}} = \dfrac{{2m}}{{1 - {m^2}}}\]
\[\dfrac{h}{{b - a}} = \dfrac{m}{{1 - {m^2}}}\]
By doing cross multiplication, we get
\[h\left( {1 - {m^2}} \right) = m\left( {b - a} \right)\]
\[h\left( {1 - {m^2}} \right) = - m\left( {a - b} \right)\]
That is \[h\left( {1 - {m^2}} \right) + m\left( {a - b} \right) = 0\]
Hence, If \[y = mx\] be one of the bisectors of the angle between the lines \[a{x^2}\; - {\text{ }}2hxy{\text{ }} + {\text{ }}b{y^2}\; = {\text{ }}0\], then \[h\left( {1 - {m^2}} \right) + m\left( {a - b} \right) = 0\]
Therefore, the correct option is (C).
Note: Here, generally students solve this example without a graphical representation of the given information but it makes it easy to solve this problem using a graphical representation. Also, it is to use tangent identity to get the desired result as the slope of a line is expressed in terms of a tangent trigonometric function.
Recently Updated Pages
The maximum number of equivalence relations on the-class-11-maths-JEE_Main

A train is going from London to Cambridge stops at class 11 maths JEE_Main

Find the reminder when 798 is divided by 5 class 11 maths JEE_Main

An aeroplane left 50 minutes later than its schedu-class-11-maths-JEE_Main

A man on the top of a vertical observation tower o-class-11-maths-JEE_Main

In an election there are 8 candidates out of which class 11 maths JEE_Main

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections

NCERT Solutions for Class 11 Maths Chapter 9 Straight Lines

NCERT Solutions For Class 11 Maths Chapter 8 Sequences And Series

How to Convert a Galvanometer into an Ammeter or Voltmeter

NCERT Solutions For Class 11 Maths Chapter 12 Limits And Derivatives




