Question

If the angle between the pass axis of the polariser and the analyser is $45^\circ $ , the ratio of intensities of the transmitted light and the original light after passing through the analyser is:
A) $\dfrac{1}{2}$
B) $\dfrac{1}{3}$
C) $1$
D) $\dfrac{1}{4}$

Answer 1

Hint: As light passes through a polarising material, it gets polarised and as a result, its intensity changes. This change is dependent on the angle between the direction of polarisation and the axis of the material. It is also dependent on the original intensity of light. The intensity $I$ of polarised light after passing through polariser and subsequently passing through analyser is;
$I = \dfrac{{{I_o}}}{2}{\cos ^2}\theta $
Where ${I_o}$ was the original intensity of light and $\theta $ is the angle between the pass axis of the polariser and the analyser.

Formulae used:
$I = \dfrac{{{I_o}}}{2}{\cos ^2}\theta $
Where ${I_o}$ the original intensity of light, $I$ is the intensity of light after passing through the polariser and the analyser and $\theta $ is the angle between the pass axis of the polariser and the analyser

Complete step by step solution:

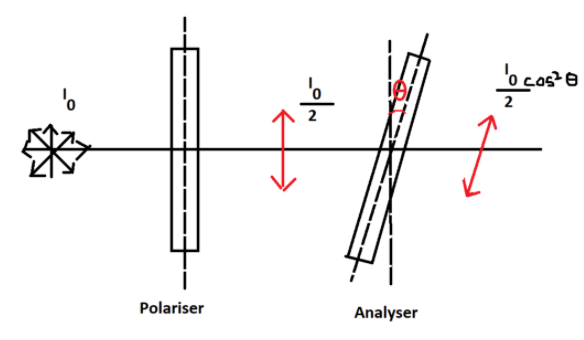
Polarisation of light is a phenomenon that occurs when unpolarised light passes through a polarising material and analyser and emerges with a particular fixed orientation in a singular plane. This leads to a change in the intensity of such a polarised light such that the new intensity is different from what the intensity of light had been before it got polarised.

In situations where unpolarised light enters a polariser and then an analyser, two separate processes occur. First the unpolarised light enters the polariser and the intensity of light changed to half of the initial value, that is,
 ${I_p} = \dfrac{{{I_o}}}{2}$ ,
where ${I_p}$ is the intensity of light after passing through the polariser
and ${I_o}$ is the original intensity of light.
This polarised light then enters the analyser before it gets transmitted and changes in accordance with the angle between the pass axis of polariser and the analyser, that is,
$I = {I_p}{\cos ^2}\theta $
$ \Rightarrow \,I = \dfrac{{{I_o}}}{2}{\cos ^2}\theta $
Where $I$ is the intensity of transmitted light.

In the given question, the angle between the pass axis of the polariser and the analyser is given as $\theta = {45^\circ }$.
Therefore, to find the intensity for the transmitted light, we use this angle in the above equation, that is,
\[I = \dfrac{{{I_o}}}{2}\cos 45^\circ \]
$ \Rightarrow I = \dfrac{{{I_o}}}{2}{(\dfrac{1}{{\sqrt 2 }})^2}$
$ \Rightarrow I = \dfrac{{{I_o}}}{2}(\dfrac{1}{2})$
$ \Rightarrow I = \dfrac{{{I_o}}}{4}$
Where $I$ is the final intensity of the transmitted light and ${I_o}$ the original intensity of light.

We have to find the ratio of final intensity of light to original intensity of light, that is,
$\dfrac{{{I_{transmitted}}}}{{{I_{original}}}} = \dfrac{I}{{{I_o}}}$
$ \Rightarrow \dfrac{I}{{{I_o}}} = \dfrac{{\dfrac{{{I_o}}}{4}}}{{{I_o}}}$
$ \Rightarrow \dfrac{I}{{{I_o}}} = \dfrac{1}{4}$

Therefore the correct answer option is (B), $\dfrac{1}{4}.$

Note: A common mistake students make is forgetting that the intensity of light gets reduced to half as it passes through the polariser. This leads to the wrong answer. To avoid such mistakes, draw the diagram given in solution to envision the polarisation of light and then proceed with the question.