Question

If in a triangle \[ABC\], the altitudes from the vertices \[A,B,C\] on opposite sides are in H.P. then \[\sin A,\sin B,\sin C\], are in
A. A.G.P.
B. H.P.
C. G.P.
D. A.P.

Answer 1

Hint:
In the given question, we need to check whether \[\sin A,\sin B,\sin C\] are in A.G.P., H.P, G.P., or A.P. For this, we have to draw a figure using the given information. Also, we need to find the area of triangle \[ABC\]. So that we will get the values of \[AD, BE, CF\]. After that, we will show \[a,b,c\] are in A.P. Finally, we will use the sine rule to get the desired result.




Formula Used:
The following formula is used for solving the given question.
In a right-angled triangle, \[Area\left( A \right) = \dfrac{1}{2} \times base \times height\]
Also, the sine rule is given by
\[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k\]
Here, \[k\] is a constant.



Complete step-by-step answer:
Consider the following figure.

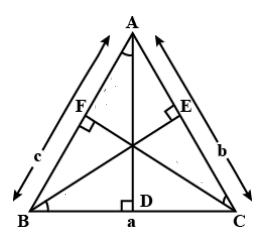
Here, \[AD, BE\] and \[CF\] are the altitudes of a triangle \[ABC\], and also they are in H.P.
Now, we will find the area of triangle \[ABC\].
\[Area\left( A \right) = \dfrac{1}{2} \times base \times height\]
\[Area\left( A \right) = \dfrac{1}{2} \times AD \times BC\]
But \[BC = a\]
So, we get \[AD = \dfrac{{2A}}{a}\]
Similarly, we get \[BE = \dfrac{{2A}}{b}\] and \[CF = \dfrac{{2A}}{c}\]
This indicates that \[\dfrac{{2A}}{a}\], \[\dfrac{{2A}}{b}\] and \[\dfrac{{2A}}{c}\] are in H.P.
Thus, we can say that \[\dfrac{1}{a}\], \[\dfrac{1}{b}\] and \[\dfrac{1}{c}\] are in H.P.
Hence, \[a\], \[b\] and \[c\] are in A.P.
Now, we will use the sine rule here.
\[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k\]
This gives, \[a = k\sin A,b = k\sin B,\]and \[c = k\sin C\]
But we know that \[a\], \[b\] and \[c\] are in A.P.
So, \[2b = a + c\]
Thus, we get \[2k\sin B = k\sin A + k\sin C\]
By simplifying, we get
\[2\sin B = \sin A + \sin C\]
Hence, \[\sin A,\sin B,\sin C\], are in A.P.
Thus, if in a triangle \[ABC\], the altitudes from the vertices \[A, B, C\] on opposite sides are in H.P. then \[\sin A,\sin B,\sin C\], are in A.P.
Therefore, the correct option is (D).

Additional Information :
A Harmonic Progression (HP) is a series of real numbers formed by calculating the reciprocals of the arithmetic progression that does not include zero. Any element in the sequence is termed the harmonic mean of its two neighbors in harmonic progression.

Note: Many students make mistake in calculation part as well as in writing the sine rule. This is the only way, through which we can solve the example in simplest way. Also, it is essential to analyse the result such as \[a\], \[b\], and \[c\] are in A.P to get the desired result.