Question

If in a triangle ABC, a = 5, b = 4, \[A = \dfrac{\pi }{2} + B\], then find C.
A. \[{\tan ^{ - 1}}\left( {\dfrac{1}{9}} \right)\]
B. \[{\tan ^{ - 1}}\left( {\dfrac{1}{{40}}} \right)\]
C. Cannot be evaluated
D. \[2{\tan ^{ - 1}}\left( {\dfrac{1}{9}} \right)\]
E. \[2{\tan ^{ - 1}}\left( {\dfrac{1}{{40}}} \right)\]

Answer 1

Hint: To solve this question, we will apply sine law in triangle ABC. In the sine law, we will substitute given data and calculate the value \[\tan B\]. Then using the value of \[\tan B\], we will calculate \[\tan A\]. By using the tangent of sum of two angles, we will calculate the value of C.

Formula used:
Sine law:
\[\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c}\]
The sum of all angles of a triangle is \[\pi \].
Tangent of sum of two angles:
\[\tan \left( {A + B} \right) = \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}}\]
Trigonometry formula:
\[\tan \left( {\dfrac{\pi }{2} + \theta } \right) = - \cot \theta \]
\[\sin \left( {\dfrac{\pi }{2} + \theta } \right) = \cos \theta \]

Complete step by step solution:

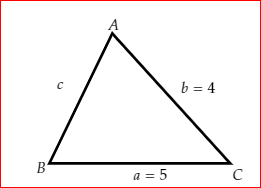
Image: Triangle ABC
Applying sine law in triangle ABC
\[\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c}\]
Substitute a = 5, b = 4, \[A = \dfrac{\pi }{2} + B\]
\[\dfrac{{\sin \left( {\dfrac{\pi }{2} + B} \right)}}{5} = \dfrac{{\sin B}}{4} = \dfrac{{\sin C}}{c}\]
Taking first two ratios
\[\dfrac{{\sin \left( {\dfrac{\pi }{2} + B} \right)}}{5} = \dfrac{{\sin B}}{4}\]
Now applying the formula \[\sin \left( {\dfrac{\pi }{2} + \theta } \right) = \cos \theta \]
\[ \Rightarrow \dfrac{{\cos B}}{5} = \dfrac{{\sin B}}{4}\]
\[ \Rightarrow \dfrac{4}{5} = \dfrac{{\sin B}}{{\cos B}}\]
\[ \Rightarrow \dfrac{4}{5} = \tan B\]
Given that, \[A = \dfrac{\pi }{2} + B\].
Take tangent both sides
\[\tan A = \tan \left( {\dfrac{\pi }{2} + B} \right)\]
Now applying \[\tan \left( {\dfrac{\pi }{2} + \theta } \right) = - \cot \theta \]
\[\tan A = - \cot B\]
\[\tan A = - \dfrac{1}{{\tan B}}\]
Substitute \[\dfrac{4}{5} = \tan B\]
\[\tan A = - \dfrac{5}{4}\]
We know that, the sum of all angles of a triangle is \[\pi \].
Thus \[A + B + C = \pi \]
\[ \Rightarrow C = \pi - \left( {A + B} \right)\]
Take tangent both sides of the equation
\[ \Rightarrow \tan C = \tan \left( {\pi - \left( {A + B} \right)} \right)\]
Now applying \[\tan \left( {\pi - \theta } \right) = - \tan \theta \]
\[ \Rightarrow \tan C = - \tan \left( {A + B} \right)\]
Now applying the tangent of sum of two angles on the right side expression
\[ \Rightarrow \tan C = - \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}}\]
Now substitute \[\tan A = - \dfrac{5}{4}\] and \[\tan B = \dfrac{4}{5}\]
\[ \Rightarrow \tan C = - \dfrac{{ - \dfrac{5}{4} + \dfrac{4}{5}}}{{1 - \left( { - \dfrac{5}{4}} \right) \cdot \dfrac{4}{5}}}\]
\[ \Rightarrow \tan C = - \dfrac{{\dfrac{{ - 25 + 16}}{{20}}}}{{1 + 1}}\]
\[ \Rightarrow \tan C = - \dfrac{{ - 9}}{{2 \cdot 20}}\]
\[ \Rightarrow \tan C = \dfrac{9}{{40}}\]
\[ \Rightarrow C = {\tan ^{ - 1}}\left( {\dfrac{9}{{40}}} \right)\]
Simplify the above equation
\[ \Rightarrow C = {\tan ^{ - 1}}\left( {\dfrac{{\left( {2 \cdot \dfrac{1}{9}} \right)}}{{1 - {{\left( {\dfrac{1}{9}} \right)}^2}}}} \right)\]
Applying the formula \[2{\tan ^{ - 1}}x = {\tan ^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)\]
\[ \Rightarrow C = 2{\tan ^{ - 1}}\left( {\dfrac{1}{9}} \right)\]
Hence option D is the correct option.

Note: Students often make mistakes to apply the formula tangent inverse. They use \[2{\tan ^{ - 1}}x = {\tan ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right)\] which is an incorrect formula. The correct formula is \[2{\tan ^{ - 1}}x = {\tan ^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)\].