
If $g(t)=\,\lbrace max(t^3-6t^2+9t-3,0\,\,t \, belongs \,to [0,3])\rbrace\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lbrace\,4-t\,\,\,\,\,\,t\,belongs\,to\,(3,4)\rbrace$
Then the number of points at which $g(t)$ is non differentiable is:
(A) $1$
(B) $3$
(C) $2$
(D) $4$
Answer
222k+ views
Hint: In this question we have to find the number of points which are non-differentiable in the given equation $g(t)$ . Only we have to do is that we simply plot a graph and we know that where the function is discontinuous the points are our non-differentiable points. By which we can easily get the number of points.
Formula Used:
Common differential formula of power used, $\dfrac{d}{{dx}}({x^n}) = n{x^{n - 1}}$
Complete step by step Solution:
Firstly, we take all the data which is provided in the question, after that we will start our solution,
We had received an equation let us assume it as,
$y = ({t^3} - 6{t^2} + 9t - 3)$
By taking differentiation of the above equation with respect to x, we get that,
$\dfrac{{dy}}{{dx}} = \dfrac{d}{{dx}}({t^3} - 6{t^2} + 9t - 3)$
By using differential identity in the above equation,
Identity used $\dfrac{d}{{dx}}({x^n}) = n{x^{n - 1}}$
As per doing further solutions we get,
$\dfrac{{dy}}{{dx}} = 3{t^2} - 12t + 9$
As we take differentiable as $y^{'}$ and taking common in the above equation,
$y^{'} = 3({t^2} - 4t + 3)$
By doing factorize in the above equation we get the values of points which we have to plot on a graph,
As per doing a further calculation of factorization,
$y^{'} = 3(t - 1)(t - 3)$
By putting t’s value in 2nd equation given in the question, we get the values for plotting the graph,
As after which get all data, we have plotted the graph which is given below,
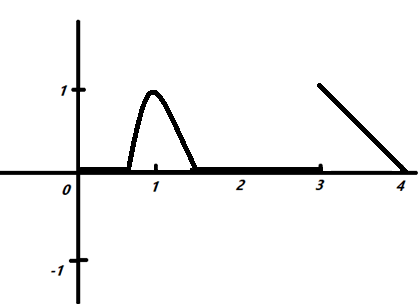
As per we get detail from the graph that there are $3$ points where the function is discontinuous.
Therefore, the answer is $3$.
Hence, the correct option is (B).
Note:As per in this question repeat gets to know that the question must be easier when the values are obtained and put on the graph whereas if we do this question only by calculation then there may or may not be any error from which I can suggest to always do this type of question by using graphical method.
Formula Used:
Common differential formula of power used, $\dfrac{d}{{dx}}({x^n}) = n{x^{n - 1}}$
Complete step by step Solution:
Firstly, we take all the data which is provided in the question, after that we will start our solution,
We had received an equation let us assume it as,
$y = ({t^3} - 6{t^2} + 9t - 3)$
By taking differentiation of the above equation with respect to x, we get that,
$\dfrac{{dy}}{{dx}} = \dfrac{d}{{dx}}({t^3} - 6{t^2} + 9t - 3)$
By using differential identity in the above equation,
Identity used $\dfrac{d}{{dx}}({x^n}) = n{x^{n - 1}}$
As per doing further solutions we get,
$\dfrac{{dy}}{{dx}} = 3{t^2} - 12t + 9$
As we take differentiable as $y^{'}$ and taking common in the above equation,
$y^{'} = 3({t^2} - 4t + 3)$
By doing factorize in the above equation we get the values of points which we have to plot on a graph,
As per doing a further calculation of factorization,
$y^{'} = 3(t - 1)(t - 3)$
By putting t’s value in 2nd equation given in the question, we get the values for plotting the graph,
As after which get all data, we have plotted the graph which is given below,
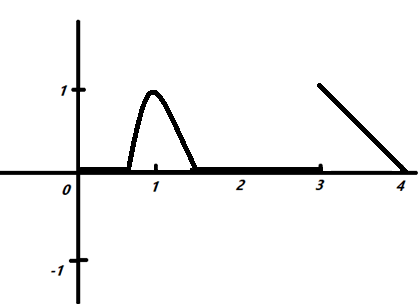
As per we get detail from the graph that there are $3$ points where the function is discontinuous.
Therefore, the answer is $3$.
Hence, the correct option is (B).
Note:As per in this question repeat gets to know that the question must be easier when the values are obtained and put on the graph whereas if we do this question only by calculation then there may or may not be any error from which I can suggest to always do this type of question by using graphical method.
Recently Updated Pages
States of Matter Chapter For JEE Main Chemistry

Mutually Exclusive vs Independent Events: Key Differences Explained

Area vs Volume: Key Differences Explained for Students

Conduction Explained: Definition, Examples & Science for Students

Balancing of Redox Reactions - Important Concepts and Tips for JEE

Atomic Size - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

How to Convert a Galvanometer into an Ammeter or Voltmeter

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Understanding the Electric Field of a Uniformly Charged Ring

Understanding Atomic Structure for Beginners

Understanding Electromagnetic Waves and Their Importance

Understanding Collisions: Types and Examples for Students




