




A Brief Introduction to Atomic Size
Measuring the atomic size is very difficult, as atoms are tiny particles with a radius range of $1.2\times10^{-10}~m$. The distance from the centre of the nucleus to the outermost shell of an atom is known as the ‘atomic radius’. Generally, the positions of the electrons are described as probability distributions that taper off gradually as the electron moves away from the nucleus. These are called ‘atomic orbitals’ or ‘electron clouds’. Thus, the precise measurement of the atomic radius is difficult as the electron cloud surrounding the atom has no sharp boundaries.
The isolation of individual atoms also makes measuring the radii a difficult task. Hence, the atomic radius is measured based on the chemically bonded state. The atomic radii of various elements can be measured by X-ray or other spectroscopic methods.
Relation Between Principal Quantum Number and Atomic Radius
The radius of an atom is the distance between the nucleus's centre and the electrons in the last orbit. However, quantum mechanics states that there is no certainty about the exact position of electrons at any time. In theory, an electron can be very close to the nucleus at one point and very far away from the nucleus at another. Since the most probable distance between the nucleus and the electrons is described by the principal quantum number(n), a larger value of the principal quantum number implies a greater distance between the electron and the nucleus. The principal quantum number(n) can be any integer with a positive value equal to or greater than one.
The principal quantum number (n) signifies the atomic size. The radius of n Bohr's orbit in terms of principal quantum number is given by the following expressions:
$r=\dfrac{n^{2} h^{2}}{4 \pi^{2} \mathrm{me}^{2}} \times \dfrac{1}{Z}=0.529 \times \dfrac{n^{2}}{Z}$
Where, n = principal quantum number of orbit
Z is atomic number
h is planck's constant
e is the elementary charge
m is the rest mass of electron
It is the radius of the lowest energy electron orbits which the Bohr model of the atom gave. Here, the radius is directly proportional to the square of the principal quantum number. The three main different types of atomic radius are
Van der Waals radius
Covalent radius
Metallic radius
Types of Atomic Radii
Van der Waals Radius: It is defined as half the minimum distance between the nuclei of two atoms of the element that are not bonded by covalent/metallic/ionic interactions. It can be used in elements where Van der Waals forces are dominated, compared to other interactions. These interactions are due to the quantum fluctuations of atomic polarisation. Van der Waals radius is most commonly applied to nonmetals (covalent compounds) and noble gases.
Van der Waals radius = $\dfrac{1}{2} \times d$
Where d = internuclear distance between two non-bonded neighbouring atoms.
Let's take the example of chlorine where the intermolecular distance between adjacent chlorine atoms is 360pm.
van der Waals radius = $\dfrac{360}{2} = 180 \mathrm{pm}$
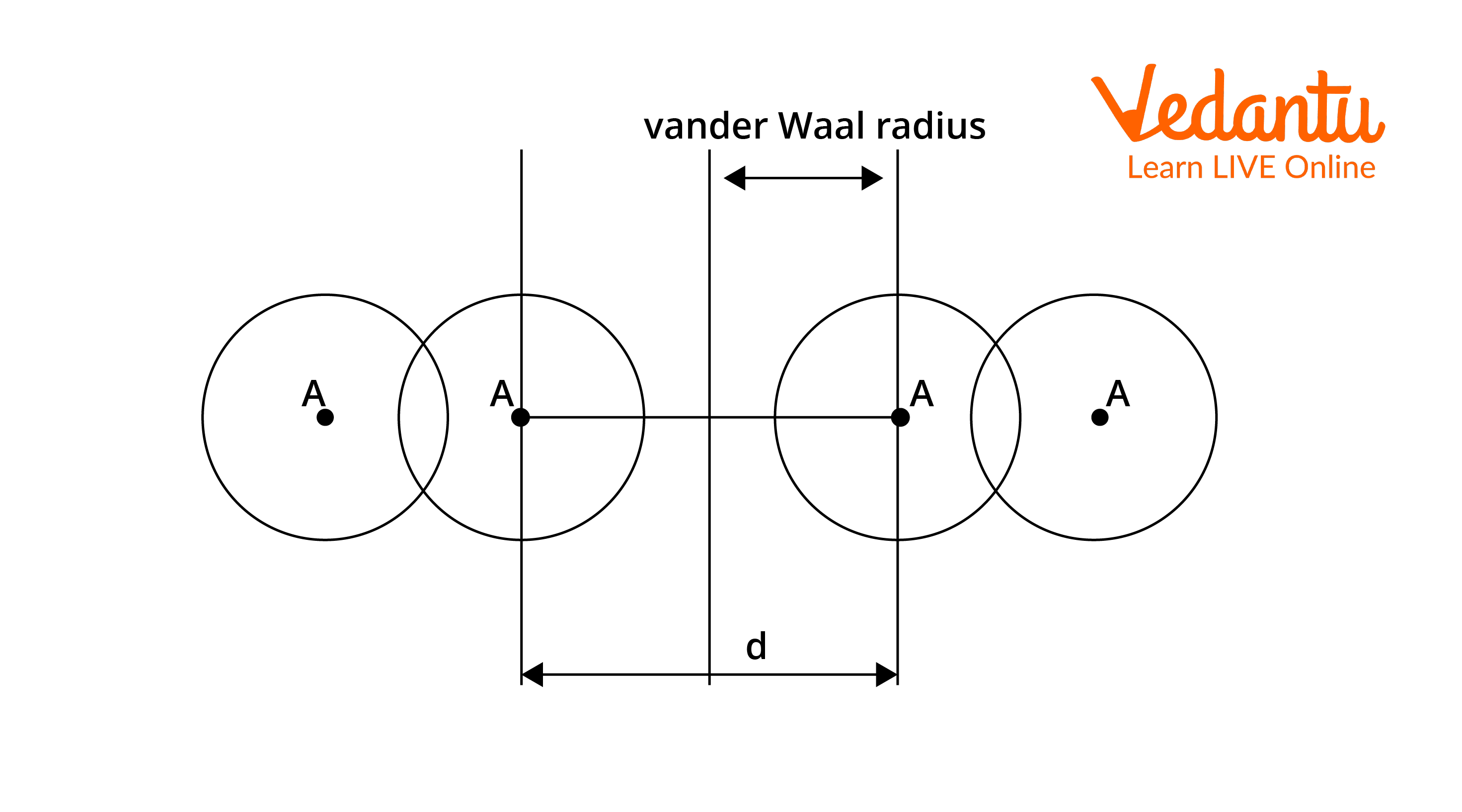
Van Der Waals Radius
In the case of helium and other inert gases, we can calculate Van der Waals radius. This is because noble gases do not form (or do not form easily) bonds. Also, the noble gases have extremely low chemical reactivity and their measured atomic radii are non-bonded. As a result, their Van der Waals radius is calculated.
Covalent Radius: The atomic radii of an element can be measured by the distance between two atoms when they have a single covalent bond in its molecules. This will give the ‘covalent radius’ of the element. It is the radius of the atoms of an element when covalently bound to other atoms, as deduced from the separation between the atomic nuclei in the molecules. In principle, the length of the covalent bond should equal the sum of their covalent radii. For example, the chlorine molecule has a bond distance of 198 pm in its molecule and the atomic radius of chlorine is half of this distance, which is 99 pm.
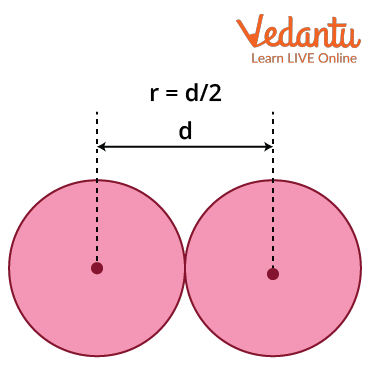
Covalent Radius
The atomic radius formula for covalently bonded atoms is given by the following equation:
rcov = $\dfrac{d}{2}$
Here, d= internuclear distance between covalently bonded atoms.
Metallic Radius: It is the nominal radius of the atoms of an element when they have metallic bonds between atoms. The metallic radius is half of the internuclear distance, which separates the metal cores in the metallic crystal. For example, in solid copper, the distance between two adjacent copper atoms is 256 pm. Hence, the metallic radius of copper is half of this distance, which is 128 pm.

Metallic Radius
Ionic Radius: The ionic radius is calculated by measuring the distance between the cations and the anions in the ionic crystal. It is the effective distance from one atomic nucleus of an ion to the electrons in the outer shell that can affect the bond formation. The size of a cation will be smaller compared to its parent atom because it has a smaller number of electrons, while its nuclear charge remains the same. An anion will be larger than its parent atom. This is because the additional electrons would cause an increased repulsion among the electrons. Hence, the effective nuclear charge will decrease.
There are atoms and ions that have the same number of electrons and are called 'isoelectronic species.’ For example, O2-, F-, Na+ and Mg2+ have the same number of electrons, i.e. 10. They have different nuclear charges, and hence their atomic radii would be different. The size of isoelectronic ions decreases as the nuclear charge increases.
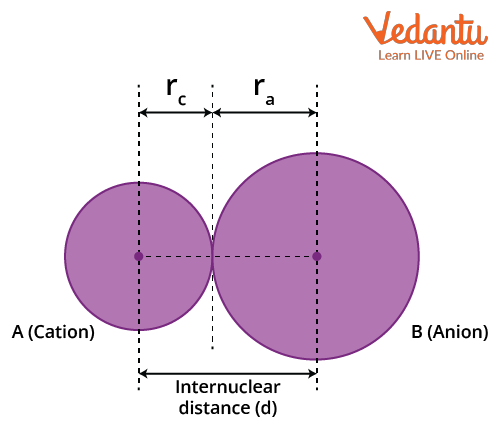
Ionic Radius
Periodic Trends in Atomic Size
Based on the variation in the nuclear charge, we can explain trends in atomic size through a periodic table. Before going ahead, we should know the difference between a nuclear charge and an effective nuclear charge. A nuclear charge is the total charge of the nucleus, which depends only on the number of protons, whereas an effective nuclear charge is a net charge that an outer shell electron experiences in an atom.
The atomic radius of elements generally decreases across a period, as illustrated in the table below. Atoms in the same period have their outer electrons in the same valence shell. Across the period, as the atomic number increases, the increasing number of electrons are added to the same valence shell. Consequently, the effective nuclear charge (the net positive charge experienced by an electron) increases. This results in an increased force of attraction between the -ve charges of electrons and the +ve charges of the nucleus. In other words, the electron cloud is pulled closer to the nucleus, and the atomic size decreases. This is shown in the table below.
Atomic Radii Across the Period
As we move down a group, the atomic radius of the elements increases. While going from one atom to another, the principal quantum level increases, but the number of electrons in the outermost shell remains the same. Hence, the effect of an increase in the size of the electron cloud is more pronounced than the effect of an increased nuclear charge. Therefore, the distance of the outermost electron from the nucleus gradually increases down the group. In other words, the size of the atom goes on increasing as we move down a group.
Atomic Radii Down the Group
The exception to the periodic trends discussed above is shown by the elements immediately following the lanthanides (lanthanum to Lutetium). They have atomic radii that are smaller than what would be expected. The effect is due to the poor shielding of the nuclear charge by 4f electrons. Hence, the 6s electrons are drawn towards the nucleus. This results in a smaller atomic radius. This effect is called ‘lanthanide contraction.’
The periodic table, atomic radius trends in noble gases show a higher increase in the atomic radius down the group. This happens because the noble gases are monatomic gases with filled outer shells and the Van der Waals radii must be considered here, which is always higher.
In the periodic table, helium has the smallest atomic radius. In helium, the effective nuclear charge that holds the valence electrons close to the nucleus is higher. Francium is the element that has the largest atomic size on the periodic table.
The atomic radius of hydrogen is 53 pm, which is higher than that of helium (31 pm). This is because the attractive force between the nucleus and the electrons in helium will be greater as it has two K shell electrons compared to one K shell electron for hydrogen. This will lead to pulling the valence shell towards the nucleus more effectively. Hence, helium has the smallest atomic size.
Conclusion
The atomic radius is calculated as the distance between the two nuclei of the atoms that are bonded together. There are mainly three types of atomic radius. They are van der Waals, covalent, and metallic radius. The atomic sizes of different elements show periodic trends. In a group, the atoms present below show an increase in atomic size as the valence shells are far away from the nucleus. On moving across a period, the atoms show a decrease in atomic size. This is mainly due to the increase in atomic number, because of which the magnitude of nuclear charge increases by a unit. Simultaneously, the addition of incoming electrons takes place in the same principal shell. As we discussed, electrons in the same shell do not screen each other from the nucleus. As a result, electrons are pulled closer to the nucleus by increased effective nuclear charge, thereby causing a decrease in the size of an atom.
FAQs on Atomic Size - JEE Important Topic
1. What is Bohr's radius?
It is the radius of the lowest-energy electron orbit as predicted in the Bohr model of the atom. Generally, it is applied to atoms and ions with a single electron, such as hydrogen and singly ionised helium. This model is now considered obsolete. However, the Bohr radius for a hydrogen atom is a physical constant. It is the most probable distance between the nucleus and electron of a hydrogen atom in its ground state. Its value is 5.29 x 10-11 m.
2. What is a d-block contraction?
The d-block contraction is due to a fully filled d orbital which has a poor shielding effect. It is used to describe the effect of having full d orbitals on the period 4 elements. The Period 4 elements with this effect are gallium, germanium, arsenic, selenium, bromine, and krypton. They have filled d orbital electronic configurations. The poor shielding of the nuclear charge by the electrons in the d orbitals causes more attraction of the nucleus towards the valence electron. This leads to an increase in ionisation potentials and also affects the atomic radius.


































