Question

If \[f(x) = a + bx + c{x^2}\], where $c > 0$ and \[{b^2} - 4ac < 0\], then the area enclosed by the coordinate axes, the line $x = 2$ and the curve $y = f\left( x \right)$ is given by
A) \[\dfrac{1}{3}\{ 4f\left( 1 \right) + f\left( 2 \right)\} \]
B) \[\dfrac{1}{2}\{ f\left( 0 \right) + 4f\left( 1 \right) + f\left( 2 \right)\} \]
C) \[\dfrac{1}{2}\{ f\left( 0 \right) + 4f\left( 1 \right)\} \]
D) \[\dfrac{1}{3}\{ f\left( 0 \right) + 4f\left( 1 \right) + f\left( 2 \right)\} \]

Answer 1

Hint:In this question, we are given the equation of the line $x = 2$ and the curve $y = f\left( x \right)$ where \[f(x) = a + bx + c{x^2}\]. Also, $c > 0$ and \[{b^2} - 4ac < 0\]. Firstly, calculate the area of the bounded area by integrating the equation of the curve from $0$ to $2$. Then, put $x = 0,1,2$ in \[f(x) = a + bx + c{x^2}\]. Then put in each option to check which of the following matches the required area.

Formula Used: Integration formula –
$\int {cdx = cx} $ where $c$ is the constant
$\int {{x^n}dx = \dfrac{{{x^{n + 1}}}}{{n + 1}}} $

Complete step by step Solution:
Given that,
\[f(x) = a + bx + c{x^2}\] where $c > 0$ and \[{b^2} - 4ac < 0\]
Therefore, to calculate the area bounded by the line $x = 2$ and the curve \[y = a + bx + c{x^2}\]
Integrate the equation of the curve from $x = 0$ to \[x = 2\] (as shown in figure 1)
 
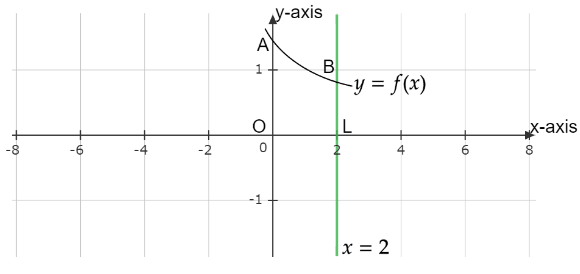
Figure 1: A graph contains the plot of the given curve and the line
So, the area of the region OLAB will be
$A = \int\limits_0^2 {\left( {a + bx + c{x^2}} \right)dx} $
As we know that, $\int {cdx = cx} $ where $c$ is the constant and $\int {{x^n}dx = \dfrac{{{x^{n + 1}}}}{{n + 1}}} $
So, $A = \left[ {ax + \dfrac{{b{x^2}}}{2} + \dfrac{{c{x^3}}}{3}} \right]_0^2$
Now, resolving the limits
We get, $A = a\left( 2 \right) + \dfrac{{b{{\left( 2 \right)}^2}}}{2} + \dfrac{{c{{\left( 2 \right)}^3}}}{3} - \left( {a\left( 0 \right) + \dfrac{{b{{\left( 0 \right)}^2}}}{2} + \dfrac{{c{{\left( 0 \right)}^3}}}{3}} \right)$
$A = 2a + 2b + \dfrac{{8c}}{3}$
Taking $\dfrac{1}{3}$ common from the whole term,
It will be, $A = \dfrac{1}{3}\left( {6a + 6b + 8c} \right)$
As we know that \[f(x) = a + bx + c{x^2}\]
At $x = 0$, we get $f\left( 0 \right) = a$
At $x = 1$, we get $f\left( 1 \right) = a + b + c$
At $x = 2$, we get $f\left( 2 \right) = a + 2b + 4c$
Now, in options (B) and (C) $\dfrac{1}{2}$ is common but according to the area we need $\dfrac{1}{3}$ to be common. So, Options (B) and (C) are not correct.
Let’s check for the remaining options
Option (A)
\[ = \dfrac{1}{3}\{ 4f\left( 1 \right) + f\left( 2 \right)\} \]
Substitute the required values,
It will be,
\[ = \dfrac{1}{3}\{ 4a + a + b + c\} \]
\[ = \dfrac{1}{3}\{ 5a + b + c\} \]
Which is not an equation to the required area.
So, Option (A) is an incorrect answer.
For Option (D),
 \[ = \dfrac{1}{3}\{ a + 4\left( {a + b + c} \right) + \left( {a + 2b + 4c} \right)\} \]
\[ = \dfrac{1}{3}\{ a + 4a + 4b + 4c + a + 2b + 4c\} \]
On solving we get, \[\dfrac{1}{3}\{ 6a + 6b + 8c\} \] which is equal to the required area.

Therefore, the correct option is (D).

Note:Different methods are used to determine the area under the curve, with the antiderivative method being the most prevalent. The area under the curve can be calculated by knowing the curve's equation, borders, and the axis surrounding the curve. There exist formulas for obtaining the areas of regular shapes such as squares, rectangles, quadrilaterals, polygons, and circles, but no formula for finding the area under a curve. The integration procedure aids in solving the equation and determining the required area. Antiderivative methods are highly useful for determining the areas of irregular planar surfaces.